欧拉工程第70题：Totient permutation

题目链接

和上面几题差不多的

Euler's Totient function, φ(n) [sometimes called the phi function]：小于等于n的数并且和n是互质的数的个数

存在这样的数：N的欧拉数φ(n)，是Ｎ的一个排列

例如：φ(87109)=79180

求在１－－－１０＾７中n/φ(n) 取到最小的 n 是多少？

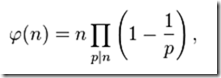
这里的是p是n的素因子，当素因子有相同的时候只取一个

任意一个正整数都能分解成若干个素数乘积的形式

直接利用上题的ｐｈｉ函数就可以求解

这个是跑的最快的函数了

long phi2(long n){
        long res = 0;
        if(n==1) return 0;
        int pi=2;
        res = n;
        while(pi*pi <=n){
            if(n%pi==0){
                res/=pi;
                res*=(pi-1);
                while(n%pi==0){
                    n/=pi;
                }
                }
            pi++;
        }
        if(n>1){
            res/=n;
            res*=(n-1);
        }
        return res;
    }
//    8319823
//    running time=89s43ms

运行结果也90s了

然后考虑到

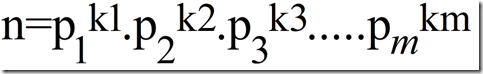
这里的pi都是素数

所以我们可以只考虑素数的情况

当n%pi==0的时候这个pi就符合条件，并去重

void run2(){
        long Max_n = 10000000;
        int Prime_len=400;
        int[] Prime = new int[Prime_len];
        Prime[0] = 2;
        int k=1;
        int p=1;
        while(k<Prime_len){
            if(isPrime(p)){
                Prime[k++] = p;
            }
            p+=2;
        }

        long result = 0;
        double minvalue=10000;
        long euler = 0 ;
        for(long n = 2;n<Max_n;n++){
            euler = phi3(n,Prime);
            if(isPerm(euler,n)){
                double temp = n/(euler*1.0);
                if(temp<minvalue){
                    minvalue = temp;
                    result = n;
                }
            }
        }
        System.out.println(result);

    }

结果：

//    8319823
//    running time=58s426ms

时间少了30s

这里缺点是要取多少个素数？

我从100,200,300,400，在400的时候结果是正确的

全部程序：

package project61;

public class P70{
    void run2(){
        long Max_n = 10000000;
        int Prime_len=400;
        int[] Prime = new int[Prime_len];
        Prime[0] = 2;
        int k=1;
        int p=1;
        while(k<Prime_len){
            if(isPrime(p)){
                Prime[k++] = p;
            }
            p+=2;
        }

        long result = 0;
        double minvalue=10000;
        long euler = 0 ;
        for(long n = 2;n<Max_n;n++){
            euler = phi3(n,Prime);
            if(isPerm(euler,n)){
                double temp = n/(euler*1.0);
                if(temp<minvalue){
                    minvalue = temp;
                    result = n;
                }
            }
        }
        System.out.println(result);

    }
//    8319823
//    running time=58s426ms

    long phi3(long n,int[]  Prime){
        long res = 0;
        if(n==1) return 0;
        int len = Prime.length;
        res = n;
        int i=0; //&& n>=Prime[i]
        while(i <len && n>=Prime[i] ){
            if(n%Prime[i]==0){
                res/=Prime[i];
                res*=(Prime[i]-1);
                while(n%Prime[i]==0){
                    n/=Prime[i];
                }
                }
            i++;
        }
        if(n>1){
            res/=n;
            res*=(n-1);
        }
        return res;
    }
    void run(){
        long Max_n = 10000000;
        long result = 0;
        double minvalue=10000;
        long euler = 0 ;
        for(long n = 2;n<Max_n;n++){
            euler = phi2(n);
            if(isPerm(euler,n)){
                double temp = n/(euler*1.0);
                if(temp<minvalue){
                    minvalue = temp;
                    result = n;
                }
            }
        }
        System.out.println(result);
    }
    boolean isPerm(long a,long b){
        int[] label = new int[10];
        while(a!=0&&b!=0){
            label[(int) (a%10)]+=1;
            label[(int) (b%10)]-=1;
            a/=10;
            b/=10;

        }
        if(a!=0) return false;
        if(b!=0) return false;
        for(int i=0;i<10;i++)
            if(label[i]!=0)
                return false;
        return true;
    }

    boolean isPrime(int n){
        if(n==2||n==3||n==5||n==7||n==11) return true;
        if(n<2||n%2==0||n%3==0) return false;
        for(int i=5;i<=Math.sqrt(n)+1;i++){
            if(n%i==0) return false;
        }
        return true;
    }

    long phi2(long n){
        long res = 0;
        if(n==1) return 0;
        int pi=2;
        res = n;
        while(pi*pi <=n){
            if(n%pi==0){
                res/=pi;
                res*=(pi-1);
                while(n%pi==0){
                    n/=pi;
                }
                }
            pi++;
        }
        if(n>1){
            res/=n;
            res*=(n-1);
        }
        return res;
    }
//    8319823
//    running time=89s43ms
//

    public static void main(String[] args){

        long start = System.currentTimeMillis();
        new P70().run2();
        long end = System.currentTimeMillis();
        long time = end - start;
        System.out.println("running time="+time/1000+"s"+time%1000+"ms");

    }
}

一直感觉这个程序还可以优化

是否还有好的算法

在解题论坛上，有个解答程序看不懂，然后我就敲成java，用时8s。。。快了好多的

long[] cal_phi(){
        long[] phi=new long[Max_n+1];
        for(int i=1;i<Max_n;i++){
            phi[i]+=i;
            for(int j=2*i;j<Max_n;j+=i)
                phi[j]-=phi[i];
        }
        return phi;
    }

8s

这个是产生Max_n的所以的欧拉函数，这个虽然是两层循环，但是效率很高的，变量完就得到欧拉函数值

下面一种形式：

long[] cal_phi2(){
        long[] phi = new long[Max_n+1];
        for(int i=1;i<Max_n;i++)
            phi[i] = i;
        for(int i=2;i<Max_n;i++){
            if(phi[i]==i)
                phi[i] = i - 1;
            for(int j=2*i;j<Max_n;j+=i)
                phi[j]*=(1-1.0/i);
        }
        return phi;
    }

15s

//    8319823
//    running time=14s577ms

至于上面是何总介绍？我还不明白

在解题报告中，还有一种是利用到素数，奇数，偶数还不明白为什么的。

全部程序：

package project61;

public class P70_1{
    int Max_n = 10000000;
    void run(){
        long[] phi=cal_phi();
        int result = 0;
        double minvalue = 10000.0;
        for(int n=2;n<Max_n;n++){
            long euler = phi[n];
            if(isPerm(euler,n)){
                double temp = n/(euler*1.0);
                if(temp<minvalue){
                    minvalue = temp;
                    result = n;
                }
            }

        }
        System.out.println(result);

    }

    long[] cal_phi(){
        long[] phi=new long[Max_n+1];
        for(int i=1;i<Max_n;i++){
            phi[i]+=i;
            for(int j=2*i;j<Max_n;j+=i)
                phi[j]-=phi[i];
        }
        return phi;
    }
//    8319823
//    running time=7s855ms
    long[] cal_phi2(){
        long[] phi = new long[Max_n+1];
        for(int i=1;i<Max_n;i++)
            phi[i] = i;
        for(int i=2;i<Max_n;i++){
            if(phi[i]==i)
                phi[i] = i - 1;
            for(int j=2*i;j<Max_n;j+=i)
                phi[j]*=(1-1.0/i);
        }
        return phi;
    }
//    8319823
//    running time=14s577ms
    boolean isPerm(long a,long b){
        int[] label = new int[10];
        while(a!=0&&b!=0){
            label[(int) (a%10)]+=1;
            label[(int) (b%10)]-=1;
            a/=10;
            b/=10;

        }
        if(a!=0) return false;
        if(b!=0) return false;
        for(int i=0;i<10;i++)
            if(label[i]!=0)
                return false;
        return true;
    }

    boolean isPrime(long n){
        if(n==2||n==3||n==5||n==7) return true;
        if(n<2||n%2==0||n%3==0) return false;
        for(int i=5;i<=Math.sqrt(n);i++)
            if(n%i==0) return false;
        return true;
    }
    public static void main(String[] args){
        long start = System.currentTimeMillis();
        new P70_1().run();
        long end = System.currentTimeMillis();
        long time = end - start;
        System.out.println("running time="+time/1000+"s"+time%1000+"ms");
    }
}

上面的程序用Python实习时间好长的