COGS103&tyvj1899 [NOIP2002]矩形覆盖

题目里给的范围是k<=4,但是官方数据并没有k==4的情况,导致一些奇奇怪怪的DP写法也能过。听说标程在k==4的时候有反例，掀桌….. 难怪COGS上k==4的数据答案是错的。

还是好好写个搜索吧:网上写法很多.我是每次沿着一条平行于坐标轴的直线将点集分割成两部分，并枚举k个矩形如何在两边分配。边界为k==1,扫一遍所有点找到最小的矩形。细节看代码吧.

但是这个搜索我也不能保证是对的,因为k==4有可能出现这种崎岖的最优方案:不存在一条平行于坐标轴且不和任何一个矩形相交的直线将4个矩形分成两部分.例如这样的最优方案：

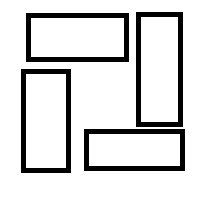
贴个代码吧:递归的时候为了处理“将点集分成两部分”调了一堆memcpy….好在递归层数和点数都不多，不然常数炸天....

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
int x[maxn],y[maxn],seq[maxn];
inline int max(int a,int b){
    return a>b?a:b;
}
inline int min(int a,int b){
    return a<b?a:b;
}
bool cmp1(const int &a,const int &b){
    return x[a]<x[b];
}
bool cmp2(const int &a,const int &b){
    return y[a]<y[b];
}
struct node{
    int x1,y1,x2,y2;
    node(){}
    node(int a,int b,int c,int d){
        x1=a;y1=b;x2=c;y2=d;
    }
}sol[];int cnt=;
int work(int l,int r,int seq[]){
    int minx=0x7f7f7f7f,miny=0x7f7f7f7f,maxx=,maxy=;
    for(int i=l;i<=r;++i){//printf("seq%d\n",seq[i]);
        minx=min(minx,x[seq[i]]);maxx=max(maxx,x[seq[i]]);
        miny=min(miny,y[seq[i]]);maxy=max(maxy,y[seq[i]]);
    }
    sol[++cnt]=node(minx,miny,maxx,maxy);
    return (maxx-minx)*(maxy-miny);
}
int s[][];int tot=;
int dfs(int l,int r,int k,int seq[]){//printf("%d\n",k);
    if(k==){
        int tmp=work(l,r,seq);
        cnt--;
        return tmp;
    }else{
        int ans=0x7f7f7f7f;
        sort(seq+l,seq+r+,cmp1);
        for(int i=l;i<r;++i){
            for(int j=;j<k;++j){
                ++tot;
                memcpy(s[tot],seq,sizeof(int)*);
                ++tot;
                memcpy(s[tot],seq,sizeof(int)*);
                if(x[seq[i]]!=x[seq[i+]]){
                    int tmp=dfs(l,i,j,s[tot-])+dfs(i+,r,k-j,s[tot]);
                    ans=min(ans,tmp);
                }
                --tot;--tot;
                //printf("---------------\n");
            }
        }//printf("%d\n",ans);
        sort(seq+l,seq+r+,cmp2);
        for(int i=l;i<r;++i){
            for(int j=;j<k;++j){
                ++tot;
                memcpy(s[tot],seq,sizeof(int)*);
                ++tot;
                memcpy(s[tot],seq,sizeof(int)*);
                if(y[seq[i]]!=y[seq[i+]]){
                    int tmp=dfs(l,i,j,s[tot-])+dfs(i+,r,k-j,s[tot]);
                    ans=min(ans,tmp);
                }
                --tot;--tot;
                //printf("---------------\n");
            }
        }//printf("%d\n",ans);
        return ans;
    }
}
int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=;i<=n;++i){
        scanf("%d%d",x+i,y+i);
    }
    for(int i=;i<=n;++i){
        seq[i]=i;
    }
    printf("%d\n",dfs(,n,k,seq));
    return ;
}