【BZOJ 3235】 3235: [Ahoi2013]好方的蛇 （单调栈+容斥原理）

3235: [Ahoi2013]好方的蛇

Time Limit: 10 Sec  Memory Limit: 64 MB
Submit: 187  Solved: 95

Description

有一天，可爱的蛇心花怒放，把自己变成了一个正方形！但是她改变的时候
被induce了导致改变出了些问题....

按照预设，她应该变成一个N*N的全黑正方形，但是这个正方形出现了一些白的格子...现在她的身体不幸出了些小反应，定义一个subsnake是一个至少有两格的全黑矩形。 

现在蛇想让你帮忙求一下一共有多少对不相交的subsnake，答案模10007。

Input

第一行一个整数 N,   接下来N行，每行一个长度为N的字符串，如果是B，那么是黑的，如果是 W那么是白的。

Output

一行一个整数，表示答案

Sample Input

3
BBW
BBW
BWW

Sample Output

5

HINT

N<=1000

Source

【分析】

　　首先考虑白点不能选。f[i][j]表示以(i,j)为左上角的矩形个数。发现这个东西其实类似有障碍点的最大子矩阵问题。【其实求和更容易一些，用一个单调栈就好了。方法自己Y吧。。

　　但是怎么统计两两不相交呢？

　　首先枚举(i,j)为左上角的矩形，右下角在其左方或上方的矩形就是不相交的。

　　但是，有可能算重复。就是这种情况：

　　

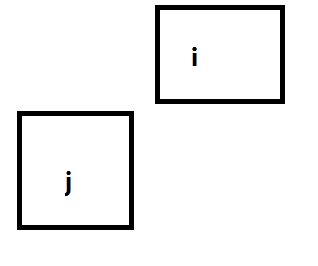
　　减掉就好了。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 #define Maxn 1010
 #define LL long long
 #define Mod 10007

 char s[Maxn][Maxn];
 int mx[Maxn][Maxn],sm[Maxn][Maxn][];
 int q[Maxn];

 int n;
 void ffind(int k)
 {
     if(k&)
     {
         for(int j=;j<=n;j++)
         {
             int l=,r=;q[]=;
             for(int i=;i<=n;i++)
             {
                 if(mx[i][j]==) {sm[i][j][k]=;q[r]=i;l=r+;continue;}
                 while(l<=r&&mx[i][j]<=mx[q[r]][j]) r--;
                 sm[i][j][k]=sm[q[r]][j][k]+(i-q[r])*mx[i][j];
                 q[++r]=i;
             }
         }
     }
     else
     {
         for(int j=;j<=n;j++)
         {
             int l=,r=;q[]=n+;
             for(int i=n;i>=;i--)
             {
                 if(mx[i][j]==) {sm[i][j][k]=;q[r]=i;l=r+;continue;}
                 while(l<=r&&mx[i][j]<=mx[q[r]][j]) r--;
                 sm[i][j][k]=sm[q[r]][j][k]+(q[r]-i)*mx[i][j];
                 q[++r]=i;
             }
         }
     }

     for(int i=;i<=n;i++) for(int j=;j<=n;j++) if(sm[i][j][k]) sm[i][j][k]--;
     if(k==) for(int i=n;i>=;i--) for(int j=;j<=n;j++)
       sm[i][j][k]=(sm[i][j-][k]+sm[i+][j][k]-sm[i+][j-][k]+sm[i][j][k])%Mod;
     else if(k==) for(int i=;i<=n;i++) for(int j=;j<=n;j++)
       sm[i][j][k]=(sm[i][j-][k]+sm[i-][j][k]-sm[i-][j-][k]+sm[i][j][k])%Mod;

 }

 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++) scanf("%s",s[i]+);

     memset(mx,,sizeof(mx));
     for(int i=;i<=n;i++) for(int j=n;j>=;j--) mx[i][j]=(s[i][j]=='W')?:mx[i][j]=+mx[i][j+];
     ffind();//zuo shang
     ffind();//zuo xia
     for(int i=;i<=n;i++) for(int j=;j<=n;j++) mx[i][j]=(s[i][j]=='W')?:mx[i][j]=+mx[i][j-];
     ffind();//you shang
     ffind();//you xia

     int ans=;
     for(int i=;i<=n;i++)
      for(int j=;j<=n;j++)
      {
          ans+=1LL*sm[i][j][]*(sm[n][j-][]+sm[i-][n][]-sm[i-][j-][])%Mod;
          ans-=1LL*sm[i][j][]*sm[i+][j-][]%Mod;
          ans%=Mod;
      }
     ans=(ans+Mod)%Mod;
     printf("%d\n",ans);
     return ;
 }

2017-04-20 10:52:07