n阶幻方问题

转载自：http://blog.csdn.net/fengchaokobe/article/details/7437767

目录
        第一节 n阶幻方问题
       第二节 由n阶幻方引发的思考

正文

第一节 n阶幻方问题

所谓n阶幻方问题，俗称“横竖斜相加和相等”（我们当时就是这么叫的）。用术语说就是：在一个N行N列的方格表中，有1，2，3......N*N-1，N*N这N*N个整数，且其对角线、横行、纵行的数字和都相等。
       好了，在具体详解该问题之前，我们先看个例子，熟悉一下，如下图所示：

 

由上图可知，幻方有奇数阶幻方和偶数阶幻方两种，而偶数阶幻方又分为4m阶幻方和4m+2阶幻方两类。

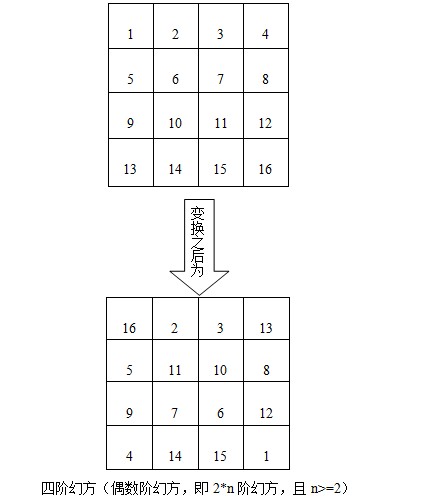
1.奇数阶幻方
       我记得基数阶幻方有个口诀，有了这个口诀，走遍奇数幻方都不怕。其实这个口诀也是实现奇数幻方的步骤。

奇幻七绝
  先填上行正中央，
  依次斜填切莫忘。
  上格没有顶格填，
  顶格没有底格放。

我作图解释一下这首七绝。

       看着图是不是有点乱，具体每一步我就不做图说明了，你自己可以看着口诀写一下，挺有意思。要是感觉3*3方格写起来没有意思，你可以试一下5*5，7*7或者更大的。写完了之后看看横竖斜相加和是否相等。
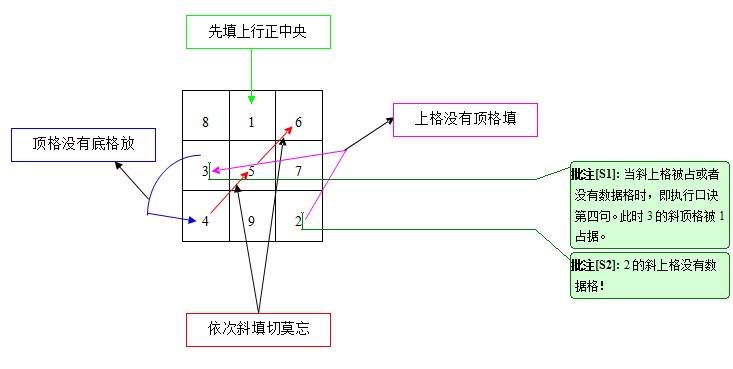
附注：如果上述口诀有什么问题，请留言说明，谢谢！
注：按我的理解就是在第一行中间填数字1，然后依次向左上角填写数字2，3，4。。。。如果当前数字的左上角已经被占用，那么就在当前数字的下方填写，再依次向左上角按顺序填写
ok，奇数幻方就讲完了，就这么简单。权当找乐子！

2.偶数阶幻方
       说实话，偶数阶幻方我一直以为只有一种，就是2*n阶幻方问题。查了一下才知道偶数阶幻方也分为两小类。

①.4*n阶幻方
       4*n阶幻方的生成其实很简单，即对方格中对角线上的数据，先以一条对角线（称对角线一）为对称轴，交换另一对角线（称对角线二）的数据；然后以对角线二为对称轴，交换对角线一的数据。说的直白一点，假设矩阵名为MagicSquare，就是交换MagicSquare[i,j]和MagicSquare[n-1-i,n-1-j]。老办法，作图来说明。图如下：

好了，4*n阶幻方也晚了，怎么样，简单吧！自己动手试试吧。

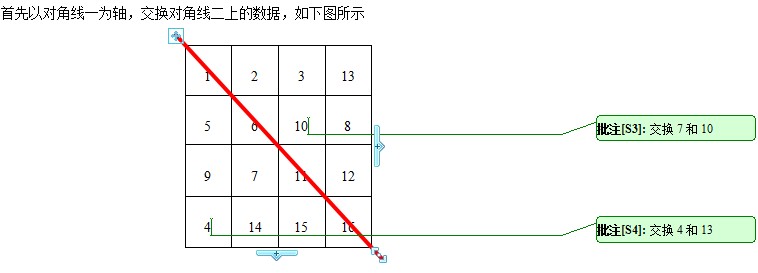
②.4*n+2阶幻方
        4*n+2，乍一看就较4*n麻烦了，事实也是如此，不过它的思想也简单。就是将4*n+2看做2*（2*n+1）,这样一来就转化成了四个2*n+1求幻方。
附注：下面的我以6阶幻方为例，那么，4*n+2=6，所以n=1。

我通过描述每个步骤加上图形的方式来表述4*n+2阶幻方实现的过程。

第一步：把整个表格分成4个（2*n+1）*（2*n+1）的小表格，分别叫A,B,C,D。见下图

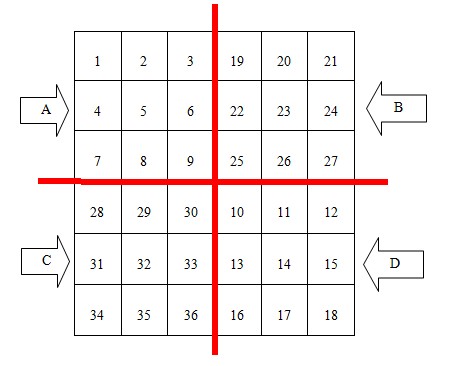
第二步：这样A,B,C,D个小表格就成奇数幻方问题了。
       ①.将1，2，...，（2*n+1）*（2*n+1）这些数划分给A，并对A实现奇数幻方;
       ②.将（2*n+1）*（2*n+1）+1,...，2*（2*n+1）*（2*n+1）这些数划分给B，并对B实现奇数幻方；
       ③.将2*（2*n+1）*（2*n+1）+1，...3*（2*n+1）*（2*n+1）这些数划分C，并对C实现奇数幻方；
       ④.将3*（2*n+1）*（2*n+1）+1，...4*（2*n+1）*（2*n+1）这些数划分D，并对D实现奇数幻方。
见下图

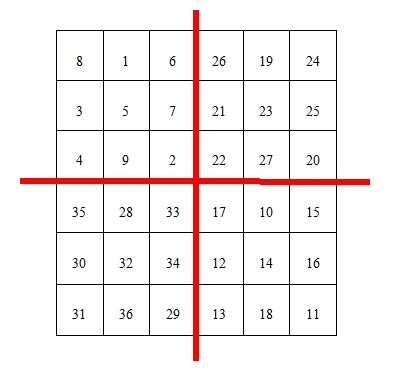
第三步：从A表中的中心（即第n行的MagicSquare[n][n]）开始，按照从左向右的方向，标出n个数，A表中的其他行则标出最左边的n格中的数（在图中用红色背景标出）。并且将这些标出的数和C表中的对应位置互换。见下图

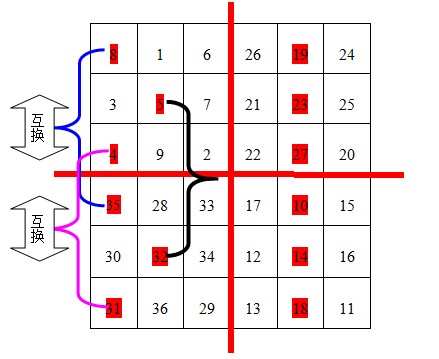
第四步：在B表中的中心（如上解释）开始，自右向左，标出n-1列，将B中标出的数据与D表中对应位置的数据交换。但是6阶幻方中，n-1此时等于0，所以B与D不用做交换。

至此，这个幻方就成了，如下图。

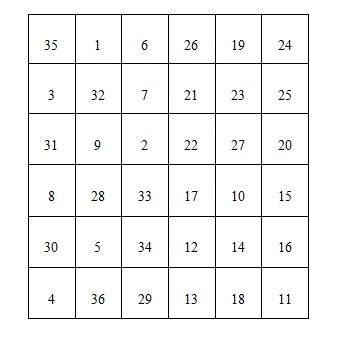
附注：以上几个问题的程序就不送上了，有兴趣的朋友可以自己写一下。

第二节 由n阶幻方想到的

幻方问题就说完了，比较一下我还是感觉奇数阶幻方有意思，而且比偶数阶幻方问题容易些，没有那么麻烦。按说写到此本应该结束了，可是我突发奇想，n阶幻方这个问题利用数学知识很容就能解决，那么我想问一下大家：在平时写程序思考算法的时候，你是否会利用数学知识来解决问题呢？

假如这个问题让你在限定的时间内编程来实现.如果你对n阶幻方很了解，知道奇偶两种情况的做法，好，那没有问题，恭喜你！但是，恰巧你对n阶幻方不是很了解，也不知道奇偶阶幻方的做法，那这个问题你会怎么解决？用枚举还是用其他什么算法。这是你不得不考虑的。

说到这，我又想到了一个例子，如：求1,2，...，99,100的和，请编程实现。你会怎么做？这个确实很简单,我相信多数朋友都会用一个for或是一个while来解决问题。那还有没有更简单的办法呢？当然有，利用数学知识来解决，1,2，...,99,100就是一个等差数列，等差数列求和的公式S=（首项+末项）*项数/2，直接得出结果。哪个效率更高，不言而喻。所以说，数学知识在我们编程中很有用，只是我们经常考虑不到而已！

第三节 结束语

如果你有更有趣或者值得深思的题目请分享!