hdu1693插头dp(多回路)

题意：在n*m的矩阵中，有些格子有树，没有树的格子不能到达，找一条或多条回路，吃全然部的树，求有多少中方法。

这题是插头dp，刚刚学习，不是非常熟悉，研究了好几天才明确插头dp的方法，他们老是讲一些什么轮廓线啊，插头啊什么的，刚開始全然不知道这些事干什么的，看完cdq的大作后也是一头的雾水，看代码，绘图，一步一步的推，最终明确了，那个是为什么，这里讲一讲。

轮廓线表示的是当前插头的状态，这题中状态中1表示有插头，0表示无插头，假设是横线的话就是上面的格子与以下的格子相连的状态，这题中显然一个格子中要码有两个插头（经过这个格子），要码没有插头（不经过这个格子），由于不可能分叉走，每一个格子走一次。

这个状态表示（101111），当前决策格子是第二行第三个格子，显然它已经有了两个插头，也就是有1条线穿过它，所以不用再加插头了。

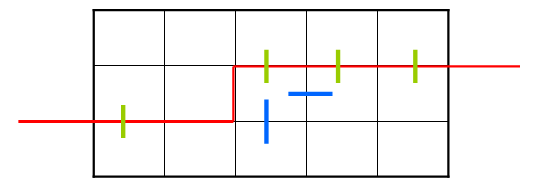
这个状态是（100111）和（101011）,当前决策格子是第二行第三个格子,显然有一个插头了，再加入一个就可以，那么就有两个选择，要码向下，要码向右，就要有两个转移。

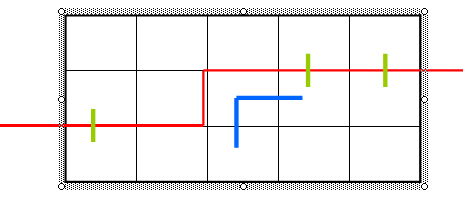
这个状态是（100011）,当前决策格子是第二行第三个格子,显然之前没有有一个插头了，仅仅能加入两个，或者不加入，不加入，就肯定不经过这个格子，显然仅仅能这个格子是不可行的。

你自己推理一下，为什么要从i，j-1个格子中状态转移过来和上一层的状态转移到下层，你会发现轮廓线的美妙。

自己用笔画画吧，好记性不如烂笔头。

我參考的代码是 http://hi.baidu.com/fqq11679/blog/item/423bcd4a3d956bf983025c6d.html

只是状态转移上有点差别，他是当前状态转到后来状态，我是当前状态从前面转来。

//hdu1693  by huicpc0207
#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
const int N=13;
const int M=(1<<N);
typedef long long LL;
LL dp[N][N][M];
int n,m,g[N][N],cas;
void read()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&g[i][j]);
}
void solve()
{
    read();
    memset(dp,0,sizeof dp);
    dp[0][m][0]=1;
    for(int i=1;i<=n;i++)
    {
        for(int k=0;k<(1<<m);++k)
            dp[i][0][k<<1]=dp[i-1][m][k];
        for(int j=1;j<=m;j++)
            for(int k=0;k<(1<<m+1);k++)
            {
                int x=1<<j-1;
                int y=1<<j;
                if(g[i][j]==0)
                {
                    if((k&x)==0&&(k&y)==0) dp[i][j][k]=dp[i][j-1][k];
                    else dp[i][j][k]=0;
                }
                else{
                    if((k&x)!=0&&(k&y)!=0)
                        dp[i][j][k]=dp[i][j-1][k^x^y];
                    else if((k&x)==0&&(k&y)==0)
                        dp[i][j][k]=dp[i][j-1][k^x^y];
                    else
                        dp[i][j][k]=dp[i][j-1][k]+dp[i][j-1][k^x^y];
                }
//                printf()
            }
    }
    printf("Case %d: There are %I64d ways to eat the trees.\n",++cas,dp[n][m][0]);
}
int main()
{
//    freopen("1.in","r",stdin);
    int t; cas=0;
    scanf("%d",&t);
    while(t--) solve();
    return 0;
}