Ackerman 函数

先留个简介：

函数定义:

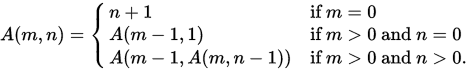
　　从定义可以看出是一个递归函数。阿克曼函数不仅值增长的非常快，而且递归深度很高。

一般用来测试编译其优化递归调用的能力。。

如果用一下代码简单实现的话，输入参数4,2程序就直接奔溃了，（复杂度太大）

#include <stdio.h>
int ackerman (int m, int n) {
    int i, tmp;
    if (m == ) return n+;
    if (n ==  && m > ) return ackerman (--m, );
    if (n >  && m >  ) {
        return ackerman (m-,ackerman(m, n-));
        }
    return ;
}

int main() {
    int m, n, acker;
    scanf("%d %d", &m,&n);
    acker = ackerman(m, n);
    printf ("%d", acker);
}