一小部分机器学习算法小结: 优化算法、逻辑回归、支持向量机、决策树、集成算法、Word2Vec等

优化算法

先导知识：泰勒公式
\[
f(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n
\]
一阶泰勒展开：
\[
f(x)\approx f(x_0)+f'(x_0)(x-x_0)
\]
二阶泰勒展开：
\[
f(x)\approx f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2}(x-x_0)^2
\]

梯度下降法

\[
\begin{align*}
&f(x)=f(x^k)+g_k^T*(x-x^k)\\
&其中，g_k=g(x^{(k)})=\nabla f(x^{(k)})=f'(x)\\
&求出第k+1次迭代值x^{(k+1)}:\ x^{(k+1)} \leftarrow x^{(k)}+\lambda_k p_k\\
&其中，p_k为搜索方向，取负梯度方向p_k=-\nabla f(x^{(k)})；\lambda_k 是步长，由一维搜索确定。\\
&即\lambda_k使得f(x^{(k)}+\lambda_kp_k)=\mathop{min}_{\lambda \geq 0}f(x^{(k)}+\lambda p_k)\\
&当||g_k||<\epsilon或者||f(x^{k+1})-f(x^k)||<\epsilon或者||x^{k+1}-x^k||<\epsilon时，停止迭代
\end{align*}
\]

注意：为何负梯度方向时是使函数值下降最快的方向，在迭代的每一步以负梯度方向更新x的值：
\[
\begin{align*}
&f(x+\Delta x)=f(x)+\sum_{k=1}^{n}\frac{\partial f}{\partial x_{k}}*\Delta x+O(||x||^n)\\
&要使f(x+\Delta x)-f(x)<0,即损失函数减小，而O(||x||^n)可忽略，则\sum_{k=1}^n\frac{\partial f}{\partial x_{k}}*\Delta x<0\\
&可以令\Delta x=-\alpha \sum_{k=1}^{n}\frac{\partial f}{\partial x_k},而\alpha为步长，\alpha>0恒成立\\
&这样就可以满足\sum_{k=1}^n\frac{\partial f}{\partial x_{k}}*\Delta x<0，因此x一直要向负梯度方向更新
\end{align*}
\]

拟牛顿法

二阶泰勒：
\[
f(x)=f(x^{k})+g_k^T*(x-x^k)+\frac{1}{2}(x-x_k)^TH(x^k)(x-x_k)\\
其中，g_k(x)=\nabla f(x^{(k)})是f(x)的梯度向量在点x^{(k)}的值。\\H(x)=\left[\frac{\partial ^2 f}{\partial x_i\partial x_j}\right]_{n*n}。后者称为海赛矩阵(Heses\ matrix)
\]

函数有极小值的必要条件是在极值点处一阶导数为0，即梯度向量为0.

可知：
\[
\nabla f(x)=g_k+H_k*(x-x^k)
\]
令$\nabla f(x)=0$，则
\[
g_k^T+H_k(x-x_k)=0\\
H_k(x-x^k)=-g_k\\
x^{k+1}=x^k-H_k^{-1}g_k
\]
令$p_k=-H^{-1}_kg_k$，即$H_kp_k=-g_k$

整理下上述思路：$f(x)$展开为二阶泰勒->函数极小值必要条件->$\nabla f(x)=0$->求得搜索方向$p_k=-H^{-1}_kg_k$

求得了搜索方向，就可以类似于梯度下降法迭代$x$的值。也就是$x^{(k+1)}=x^k+p_k$。

注意到搜索方向$p_k=-H^{-1}_kg_k$,求解公式中存在矩阵的逆，矩阵的逆一般难求，需要考虑用一个$n$阶矩阵$G_k=G(x^{(k)})$近似代替$H_k^{-1}=H^{-1}(x^{(k)})$。这就是所谓的“拟”牛顿法

首先看要近似的海塞矩阵$H_k$要满足的条件。对$\nabla f(x)=g_k+H_k(x-x^k)$取$x=x^{(k+1)}$，即得：$g_{k+1}=g_k+H_k(x^{(k+1)}-x^k)$，记$y_k=g_{k+1}-g_k,\delta_k=x^{(k+1)}-x^k$，则：
\[
y_k=H_k\delta_k
\]
这就是海塞矩阵要满足的条件。也就是$H^{-1}_ky_k=\delta_k$。根据这个条件，近似的算法有两种，也就是"DFP"算法和"BFGS"算法，以及推广的"Broyden"算法。参见《统计学习方法》-李航-p222~224

拉格朗日对偶性

约束最优化问题中，由于原始问题难求等原因，需要利用拉格朗日对偶性将原始问题转化为对偶问题，通过求解对偶问题而求得原始问题的解。

约束最优化问题：
\[
\mathop{min}_{x\in R^n}f(x)\\
s.t\quad c_j(x)\leq 0,\ i=1,2,...,k\\
h_j(x)=0,\ j=1,2,...,l
\]
其转化而得的对偶问题：广义拉格朗日函数极大极小问题
\[
\mathop{max}_{\alpha,\beta}\theta_D(\alpha,\beta)=\mathop{max}_{\alpha,\beta}\mathop{min}_xL(x,\alpha,\beta)\\
st.\quad \alpha_i\geq0,\ i=1,2,...,k
\]
KTT条件：对偶问题和原问题能够相互转化的充要条件

假设函数$f(x)$和$c_i(x)$是凸函数，$h_j(x)$是仿射函数，并且不等式约束$c_i(x)$是严格可行的，则$x^*$和$\alpha ^*,\beta ^*$分别是原始问题和对偶问题的解的充要条件是$x^ *$,$\alpha^*$,$\beta ^*$满足KTT条件：
\[
\nabla _x L(x^*,\alpha ^*,\beta ^*)=0\\
\alpha^*_ic_i(x^*)=0,\ i=1,2,...,k\\
c_i(x^*)\leq 0,\ i=1,2,...,k\\
\alpha ^*_i\geq0,\ i=1,2,...,k\\
h_j(x^*)=0,\ j=1,2,...,l
\]

李航-《统计学习方法》-p218~p228

最大似然函数和最小损失函数

当然你也可以叫它”最大似然函数和最小二乘估计“，两者殊途同归，都是意在拟合数据

最小二乘估计

模型最合理的参数估计量应该使得模型最好的拟合样本数据，要求估计值和观测值之差的平方最小。

定义：
\[
Q=\sum_{i=1}^n(y-y')^2
\]
其中，$Q$为误差，$y$为观测值，$y'$为估计值，$y'=\beta_0+\beta_1x$

矩阵表示：
\[
min||A\beta-Y||_2
\]
最优解为：
\[
\beta=(A^TA)^{-1}A^TY
\]
其中，估计值$Y'=||A\beta||$。关于求解方法参见：最小二乘法解的矩阵形式推导.若A非满秩，常常采用求伪逆的方法或者岭回归等方法解决。求伪逆，参见周志华-《机器学习》-p402~p403（A.3奇异值分解）

最大似然函数

模型最合理的参数估计量应该使得观测样本出现的概率最大。

定义：联合概率密度函数$p(D|\theta)$称为相对于${x_1,x_2,...,x_N}$关于$\theta$的似然函数
\[
l(\theta)=p(D|\theta)=p(x_1,x_2,...,x_N|\theta)=\prod_{i=1}^{N}p(x_i|\theta)
\]
其中，$\theta$为待估计参数。

与最小二乘法不同不需要确定概率分布函数不同，最大似然函数需要”已知“这个概率分布函数。事实上，若假设满足正态分布函数，最大似然函数和最小二乘估计是等价的。参见：最大似然估计和最小二乘估计的区别与联系。最小二乘法以估计值和观测值的差平方和为损失函数，最大似然函数则是以最大化似然概率函数为目标函数。

交叉熵

交叉熵衡量的是两个分布$p$、$q$之间的相似性。

定义：
\[
H(P,Q)=-\sum_{i=1}^np(x_i)log(q(x_i))
\]
其中$H(p,q)$即为交叉熵。事实上，交叉熵是由KL散度（亦称相对熵）而来，KL散度：
\[
KL(P||Q)=\int _{-\infty}^{\infty}p(x)log\frac{p(x)}{q(x)}dx
\]
展开便得：
\[
KL(P||Q)=\int_{-\infty}^{\infty}p(x)log\ p(x)dx-\int_{-\infty}^{\infty}p(x)log\ q(x) dx=-H(P)+H(P,Q)
\]
在机器学习中，常常需要评估观测值和估计值之间的差距，由于KL散度能够度量两个概率分布之间的差距，可以最小化KL散度实现“学习”的目的。又由于$H(P)$为固定值，所以通常直接最小化交叉熵$H(P,Q)$，参见周志华-《机器学习》-p414~p415(C.3KL散度)

在分类问题中，交叉熵的本质就是似然函数的最大化。参见：最大似然损失和交叉熵损失函数的联系

关于为何逻辑logistic回归采用交叉熵（似然函数）而非最小二乘作损失函数，可能有两个原因：1.交叉熵常常用于分类，而最小二乘常常用于回归；2.计算便利

逻辑回归

先导知识：

指数族分布

若某概率满足
\[
p(y;\eta)=b(y)exp(\eta^TT(y)-a(\eta))
\]
其中$\eta$是自然参数，$T(y)$是充分统计量，$exp(-a(\eta))$起到归一化作用。确定$T,a,b$，就可以确定参数为$\eta$的指数族分布。高斯分布、伯努利分布、多项分布、泊松分布等都是指数族分布的特定形式。

伯努利分布：
\[
\begin{align*}
p(y;\phi)&=\phi^y(1-\phi)^{1-y}\\
&=exp(ylog\ \phi+(1-y)log(1-\phi))\\
&=epx(ylog\frac{\phi}{1-\phi}+log(1-\phi))
\end{align*}
\]
对照上述指数族分布定义，则：
\[
\begin{equation}
\left \{
\begin{array}{lr}
T(y)=y,\\
\eta=log\frac{\phi}{1-\phi},(\frac{\phi}{1-\phi}=e^{\eta}->(1+e^y)\phi=e^y->\phi=\frac{e^{\eta}}{1+e^{\eta}}=\frac{1}{1+e^{-\eta}})\\
a(\eta)=-log(1-\phi)\\
b(y)=1
\end{array}
\right .
\end{equation}
\]
常见的概率分布参见：周志华-《机器学习》-p409~p413(C概率分布)

逻辑回归

考虑二分类问题，$y\in\{0,1\}$,因为是二分类问题，可以很自然的想到选择$p(y|x;\theta)$~$Bernouli (\phi)$，即服从伯努利分布。那么，
\[
h_\theta=E(y|x;\theta)=\phi=\frac{1}{1+e^{-\eta}}=\frac{1}{1+e^{-\theta^Tx}}
\]
其中，$h_\theta(x)=E(y|x;\theta)=\phi$是伯努利分布的性质（其数学期望等于每次实验成功的概率$\phi$），$\phi=\frac{1}{1+e^{-\eta}}$是伯努利分布为指数族分布时的结论（见$\eta=log\frac{\phi}{1-\phi}$后面推导过程）

定义：
\[
h_\theta=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}
\]
目标函数推导：
\[
\begin{equation}
\left \{
\begin{array}{lr}
p(Y=1|x;\theta)=h_\theta(x)\\
p(Y=0|x;\theta)=1-h_\theta(x)
\end{array}
\right .
\end{equation}
\]
其中，$h_\theta(x)$表示类别为1的概率。

结合起来
\[
p(Y=y|x;\theta)=(h_{\theta})^y(1-h_{\theta})^{1-y}
\]
取对数似然函数:
\[
\begin{align*}
l(\theta)&=\prod_{i=1}^m p(Y=y_i|x_i;\theta)\\
&=\prod_{i=1}^m(h_\theta(x_i))^{y_i}(1-h_\theta(x_i))^{1-y_i}
\end{align*}\\
L(\theta)=\sum_{i=1}^{m}y_ilog\ h_{\theta}(x_i)+(1-y_i)log\ (1-h_\theta(x_i))
\]
优化损失函数：
\[
J(\theta)=\frac{-1}{m}L(\theta)
\]
使用梯度下降法等优化算法优化即可。

注意此处的损失函数和交叉熵定义：$H(p,q)=-\sum_{i=1}^np(x_i)log(q(x_i))$

列出其它常见的损失函数

0-1损失函数
\[
L(y,f(x))=
\begin{equation}
\left \{
\begin{array}{lr}
1\quad y\neq f(x)\\
0\quad y=f(x)
\end{array}
\right .
\end{equation}
\]
平方损失函数
\[
L(y,f(x))=(y-f(x))^2
\]
绝对值损失函数
\[
L(y,f(x))=|y-f(x)|
\]
对数损失函数
\[
L(y,p(y|x))=-log\ p(y|x)
\]

支持向量机

先导知识：

点到直线距离公式
\[
d=|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}|=|\frac{wx_i+b}{||w||}|
\]
假设点X被正确分类。当X属于正类时，$wx+b>0$,此时点X在直线上方。当X属于负类时，$wx+b<0$，此时点X在直线下方。

几何间隔最大化
\[
\mathop{max}_{w,b}\ \gamma\\
s.t\quad \frac{y_i(wx_i+b)}{||w||}\geq \gamma,\ i=1,2,...,N
\]
这也即是，学习超平面参数$w$，使得当所有点到超平面的距离都大于某个数$\gamma$：
\[
\frac{y_i(wx_i+b)}{||w||}\geq \gamma
\]
时，最大化这个数$\gamma$。乘以$y_i$的目的在于当$y_i\in\{+1,-1\}$时，无论$wx_i+b$得到的结果无论正负，只要分类结果正确，保持$y_i(wx_i+b)$为正。

可以改写为，令函数间隔$\hat{\gamma}=y_i(wx_i+b)$，得$\gamma=\frac{\hat{\gamma}}{||w||}$，则
\[
\mathop{max}_{w,b}\frac{\hat{\gamma}}{||w||}\\
s.t\quad y_i(wx_i+b)\geq\hat{\gamma},\ i=1,2,...,N
\]
由于有分母$||w||$有规范化作用，函数间隔$\hat{\gamma}$的取值并不影响最优化问题的解，令$\hat{\gamma}=1$翻转分子分母，变最大化问题为最小化问题：
\[
\mathop{min}_{w,b}\frac{1}{2}||w||^2\\
s.t\quad y_i(wx_i+b)-1\geq 0,\ i=1,2,...,N
\]

线性可分支持向量机

硬间隔最大化

定义：
\[
\mathop{min}_{w,b}\frac{1}{2}||w||^2\\
s.t\quad y_i(wx_i+b)-1\geq 0
\]
求得最优解$w^*,b^*$。代入之后就可以求得分离超平面：$w^*x+b^*=0$；分类决策函数：$f(x)=sign(w^*x+b^*)$

线性支持向量机

软间隔最大化：正则化，引入松弛变量$\xi_i\geq0$，约束条件变为$y_i(wx_i+b)\geq 1-\xi_i$；并且对每个松弛变量$\xi_i$，支付一个代价$\xi_i$，目标函数变为$\frac{1}{2}||w||^2+C\sum_{i=0}^{N}\xi_i$，其中$C$为正则化参数。这样使得$\frac{1}{2}||w||^2$尽量小，即间隔最大而且误分类点个数尽可能少。

定义：
\[
\mathop{min}_{w,b,\xi}\frac{1}{2}||w||^2+C\sum_{i=1}^N\xi_i\\
s.t\quad y_i(wx_i+b)\geq 1-\xi_i\ i=1,2,...,N\\
\xi_i\geq0,\ i=1,2,...,N
\]
$\xi_i\geq 0$原因：1)$\xi_i\geq 0$意为允许误分点，$\xi>0$意为允许误分点，$\xi<0$在分隔界面后侧无意义。2)目标是$\mathop{min}_{w,b,\xi}$，若允许$\xi<0$则会使目标式使$\xi\to-\infty$，错误

原始最优化算法的拉格朗日函数：
\[
L(W,b,\xi,\alpha,\mu)=\frac{1}{2}||w||^2+C\sum_{i=1}^N\xi_i-\sum_{i=1}^{N}\alpha_i(y_i(wx_i+b)-1+\xi_i)-\sum_{i=1}^N\mu_i\xi_i
\]
其中，$W,b$为超平面的参数，$\alpha,\xi$为拉格朗日乘子($\alpha_i>0,\xi>0$，两个条件，两个拉格朗日乘子)

对偶问题是拉格朗日的极大极小问题
\[
\mathop{max}_\alpha \mathop{min}_{w,b} L(w,b,\alpha)
\]
首先求$L(w,b,\xi,\alpha,\mu)$对$w,b,\xi$的极小。
\[
\begin{equation}
\left \{
\begin{array}{lr}
\frac{\partial}{\partial w}L(w,b,\xi,\alpha,\mu)=w-\sum_{i=1}^N\alpha_iy_ix_i=0\\
\frac{\partial}{\partial b}L(w,b,\xi,\alpha,\mu)=-\sum_{i=1}^N\alpha_i y_i=0\\
\frac{\partial}{\partial \xi}L(w,b,\xi,\alpha,\mu)=C-\alpha_i-\mu_i=0
\end{array}
\right .
\end{equation}
\]
求得：
\[
\begin{equation}
\left \{
\begin{array}{lr}
w=\sum_{i=1}^N\alpha_i y_i x_i\\
\sum_{i=1}^{N}\alpha_i y_i=0\\
C-\alpha_i-\mu_i=0
\end{array}
\right .
\end{equation}
\]
代入$L(w,b,\xi,\alpha,\mu)$得
\[
\begin{align*}
L(w,b,\xi,\alpha,\mu)&=\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_ix_j)+C\sum_{i=1}^{N}\xi_i-\\
&\sum_{i=1}^{N}(\alpha_iy_i(wx_i+b)-\alpha_i+\alpha_i\xi_i)-\sum_{i=1}^{N}\mu_i\xi_i(1)\\
&=\frac{1}{2}\sum_{i=1}^{N}\sum_{i=1}^{N}\alpha_i\alpha_jy_iy_j(x_ix_j)+(C-\alpha_i-\mu_i)\sum_{i=1}^{N}\xi_i-\sum_{i=1}^N\alpha_i(2)\\
&=\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum_{i=1}^N\alpha_i
\end{align*}
\]
在(1)中，由于$\sum_{i=1}^N\alpha_iy_i=0$，则$\sum_{i=1}^N(\alpha_iy_i(wx_i+b))=0$

在(2)中，由于$C-\alpha_i-\mu_i=0$，则$(C-\alpha_i-\mu_i)\sum_{i=1}^{N}\xi_i=0$

得对偶问题：
\[
\begin{align*}
\mathop{max}_{\alpha}-\frac{1}{2}\sum_{i=1}^{N}\sum^{N}_{j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)+\sum_{i=1}^N\alpha_i\\
s.t\quad \sum_{i=1}^{N}\alpha_iy_i=0\quad\\
C-\alpha_i-\mu_i=0\quad(1)\\
\alpha_i\geq0\quad(2)\\
\mu_i\geq0\quad(3)\\
(i=1,2,...,N)
\end{align*}
\]
$(1),(2),(3)$可得：$0\leq\alpha_i\leq C$

也即是：
\[
\begin{align*}
\mathop{max}_{\alpha}-\frac{1}{2}\sum_{i=1}^{N}\sum^{N}_{j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)+\sum_{i=1}^N\alpha_i\\
s.t\quad \sum_{i=1}^{N}\alpha_iy_i=0\\
0\leq\alpha_i\leq C\\
(i=1,2,...,N)
\end{align*}
\]
这就是线性支持向量机的对偶问题。

有对偶问题据说易求得最优解$\alpha^*=(\alpha_1^*,\alpha_2^*,...,\alpha_N^*)$，从而求得原始问题中$w^*=\sum_{i=1}^N\alpha_i^*y_ix_i$，选择$\alpha^*$中一个适合条件$0<\alpha_j^*<C$分量$\alpha_j^*$，可得原始问题中的$b^*=y_j-\sum_{i=1}^Ny_i\alpha_i^*(x_ix_j)$。然后代入即得分离超平面：
\[
w^*x+b^*=0
\]
分类决策函数：
\[
f(x)=sign(w^*x+b^*)
\]

非线性支持向量机和核函数

举例而言，
\[
w_1(x^{(1)})^2+w_2(x^{(2)})^2+b=0
\]
此为非线性问题，使用$z=\phi(x)=(x^{(1)},x^{(2)})$映射可得
\[
w_1z^{(1)}+w_2z^{(2)}+b=0
\]
转化为了线性问题。

从输入空间x到特征空间的映射$\phi(x)$: $x$->$H$

线性支持向量机只涉及输入实例与实例之间的内积，且映射函数$\phi(x)$不易求

核函数$K(x,z)=\phi(x)·\phi(z),\quad x,z\in X$

将输入空间的内积$x_i·x_j$转化为特征空间的内积$\phi(x_i)·\phi(x_j)=K(x,z)$，此时当映射函数是非线性函数时，就可以在线性SVM中学习非线性模型了。

函数$K(x,z)$为核函数的条件

通常的核函数就是正定核函数。

正定核的充要条件：

$K(x,z)$是定义在$X*X->R$上的对称函数，则$K(x,z)$为正定核函数的充要条件：

$K(x,z)$对应的Gram矩阵：
\[
K=[k(x_i,x_j)]_{m*m}=
\left[
\begin{matrix}
(x_1,x_1)&(x_1,x_2)&(x_1,x_3)&\cdots&(x_1,x_m)\\
\vdots\\
(x_m,x_1)&(x_m,x_2)&(x_m,x_3)&\cdots&(x_m,x_m)
\end{matrix}
\right]
\]
此矩阵半正定

常用核函数

多项式核函数：$K(x,z)=(x·z+1)^p$

对应的分类决策函数为：$f(x)=sign(\sum_{i=1}^{N_c}a_i^*y_i(x_i·x+1)^p+b^*)$
高斯核函数：$K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2})$

对应的分类决策函数：$f(x)=sign(\sum_{i=1}^{N_c}a_i^*y_iexp(-\frac{||x-z||^2}{2\sigma^2})+b^*)$

此处参见李航-《统计学习方法》-p122~p123

高效实现支持向量机“学习”的算法：SMO序列最小最优化算法

SMO求解如下凸二次规划的对偶问题：
\[
\begin{align*}
&\mathop{min}_\alpha\ \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum_{i=1}^{N}\alpha_i\\
&s.t\quad \sum_{i=1}^{N}\alpha_iy_i=0\\
&0\leq \alpha_i\leq C,\ i=1,2,...,N
\end{align*}
\]
变量是拉格朗日乘子$\alpha$，一个变量$\alpha_i$对应于一个样本点$(x_i,x_j)$。变量总量等于训练样本容量$N$.

启发式算法：

若所有变量符合KTT条件，则该问题可由KTT求得（KTT条件是该最优化问题的充要条件）
否则，选择2个变量（1个最不符合KTT，另1个自动确定）构造新的二次规划问题求解。

李航-《统计学习方法》-p95

KMeans

一种聚类算法

算法流程：
\[
\begin{align*}
输入：&样本集D=\{x_1,x_2,...,x_m\};聚类簇数K\\
过程：\\
&随机初始化K个均值向量\{u_i,u_2,...,u_k\}\\
&Repeat:\\
&\quad for\ i=1,2,...,m\quad do\\
&\qquad 将距离最近的均值向量u_i作为x_i的簇标记(C_{u_{j}}=C_{u_j}\cup(x_i))\\
&\quad for\ i=1,2,..,k\quad do\\
&\qquad 计算均值均值向量u_i'=\frac{\sum_{x\in C_{u_j}}x}{|C_{u_j}|}并更新
\end{align*}
\]
总结下来就两步：1)样本划归簇标记；2)更新均值向量

KMeans算法优缺点

优点：

原理简单，超参就一个聚类簇数K
速度快

缺点：

K值需要事先确定
对初始均值向量敏感
对离群点敏感
不断对每一个样本分类调整，不断调整聚类中心，当数据量大时，时间开销大
没有先验知识。比如不能加入先验：cluster A: 500; cluster B: 1000
不能发现非凸形状的簇

决策树

生成：

假设：
- 当前节点包含的样本均属于同一个类别
- 当前节点包含的样本集合为空
- 当前属性集为空，或者所有样本在所有属性上取值相同
标注该节点为叶节点，返回
否则：
- 在每个节点上，根据特征选择规则（信息增益ID3，增益率C4.5，基尼指数CART等）选择属性，分裂节点，直到无法分裂

常见的特征选择规则：

先导知识：

信息熵$Ent(D)=-\sum_{k=1}^{|y|}p_klog\ p_k$。 $p_k$: 当前样本集合中第k类样本所占比例。

$Ent(D)$的值越小，则$D$的纯度越高。

多说一句，这和交叉熵定义很像。交叉熵：$H(p,q)=-\sum_{i=1}^np(x_i)log(q(x_i))$

信息增益$Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{D^v}{D}Ent(D^v)$

特征a上的信息增益，选择较大的特征分裂
增益率$Gain\_ratio(D,a)=\frac{Grain(D,a)}{IV(a)}$

其中，$IV(a)=-\sum_{v=1}^{V}\frac{D^v}{D}log_2\frac{D^v}{D}$称为特征a的“固有值”。

特征a上的增益率，选择较大的特征分裂
基尼值$Gini(D)=\sum_{k=1}^{|y|}\sum_{k'\neq k}p_k p_{k'}=1-\sum_{k=1}^{|y|}p_k^2$

$Gini(D)$反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。$Gini(D)$越小，数据集$D$的纯度越高。

特征a的基尼指数定义为：$Gini\_index(D,a)=\sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$

选择划分后使得，基尼指数最小的特征

集成算法

boosting：将弱学习器提升为强学习器。典型代表：AdaBoost、GBDT等，GBDT将在下面单独介绍

先从初始训练集训练出一个基学习器，根据基学习器的表现对训练样本分布进行调整，使之前错误分类的样本获得更多的“关注”，基于调整后的样本分布训练下一个基分类器，如此重复，再将T个基分类器加权结合。

AdaBoost

输入:训练数据集$T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$;弱学习算法
输出:最终分类器$G(x)$

初始化训练数据的权值分布：
\[
D_1=(w_{11},w_{12},...,w_{1N}),\quad w_{1j}=\frac{1}{N},i=1,2,...,N
\]
对$m=1,2,...,M$（训练组合M个弱分类器）：

1)使用带权值分布的$D_m$的训练数据集学习，得到基分类器$G_m(x):x\to\{-1,+1\}$

2)计算$G_m(x)$在训练数据集上的分类误差率
\[
e_m=\sum_{i=1}^{N}p(G_m(x_i)\neq y_i)=\sum_{i=1}^{N}w_{m_i}I(G_m(x_i)\neq y_i)
\]
3)计算$G_m(x)$的系数
\[
\alpha_m=\frac{1}{2}log \frac{1-e_m}{e_m}
\]
4)更新训练数据集的权值分布
\[
D_{m+1}=(w_{({m+1},1)},w_{({m+1},2)},...,w_{({m+1},N)})\\
w_{(m+1,i)}=\frac{w_{(m,i)}}{Z_m}exp(-\alpha_m y_iG_m(x_i)),\quad i=1,2,...,N
\]
其中$Z_m$为规范化系数，$Z_m=\sum_{i=1}^{N}w_{m_i}exp(-\alpha _my_iG_m(x_i))$
构建基本分类器的线性分类器：$f(x)=\sum_{m=1}^M\alpha_mG_m(x)$

最终分类器：
\[
G(x)=sign(f(x))=sign(\sum_{m=1}^M\alpha_mG_m(x))
\]

简而言之，求两个参数：训练数据的权重$D_m$和基分类器$G_m(x)$的系数$\alpha_m$

AdaBoost算法是加法模型，损失函数是指数函数，学习算法是前向分布算法时的二分类学习方法

参见李航-《统计学习方法》-p138~p142

bagging：随机森林即是bagging的一种扩展变体。

从原始数据集中采取有放回抽样，构造“采样集”，采样集$D'$的数据量是和原始数据集$D'$相同的。可采样出T个含m个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再将基学习器结合。

显然有一部分样本会在采样集$D'$中出现多次，而另一部分样本始终不出现，样本在$m$次采样中始终不被采样到的概率为：
\[
\lim_{m\to \infty}(1-\frac{1}{m})^m=\frac{1}{e}
\]
随机森林

随机性：

1)基决策树的训练数据集由bagging产生。

2)待选属性集随机产生。待选属性集由节点的属性集合中随机选择的$k$个属性组成，$k=log_2 d$，d为节点属性集合的大小

对于提升算法而言，基分类器$f$常采用回归树和逻辑回归。树模型有以下优缺点。

优点
- 可解释性强
- 具有伸缩不变性，不必归一化特征
- 对异常点鲁棒
缺点
- 缺乏平滑性。回归预测时，输出值只能输出有限的若干个数值
- 不适合处理高维度稀疏数据

gbdt和xgboost区别：

gbdt在函数空间中采用梯度下降法进行优化
xgboost在函数空间中利用牛顿法进行优化

梯度提升决策树

梯度提升决策树(Gradient Boosting Decision Tree, GBDT)

梯度提升算法利用梯度下降法的近似方法，其关键是利用损失函数的负梯度在当前模型的值，也就是
\[
-\left[ \frac{\partial L(y,f(x_i))}{\partial f(x_i)} \right]_{f(x)=f_{m-1}(x)}
\]
作为提升树算法中的残差的近似值，拟合一个回归树

模型F定义（加法模型）：
\[
F(x;w)=\sum_{t=0}^T\alpha_t h_t(x;w_t)
\]
其中$x$为输入样本，$h$是分类回归树，$w$是分类回归树的权重，$\alpha$是每棵树的权重

目标：最小化损失函数
\[
F^*=\mathop{argmin}_{F}\sum_{i=0}^N L(y_i,F(x_i;w))
\]
迭代求局部最优解

梯度提升决策树算法流程

输入：$(x_i,y_i),T$

初始化$f_0$
$for\ t=1\ to\ T\ do$
- 计算损失函数的负梯度，作为残差的近似值：$\tilde{y_i}=-\left[ \frac{\partial L(y,F(x_i))}{\partial F(x_i)} \right]_{F(x)=F_{t-1}(x)}$,其中$i=1,2,...,N$
- 学习第$t$棵树：$w^*=\mathop{argmin}_w\sum_{i=1}^{N}(\tilde{y_i}-h_t(x_i;w))$
- line search 寻找步长：$\rho^*=\mathop{argmin}_{\rho}\sum_{i=1}^NL(y_i,F_{t-1}(x_i)+\rho h_t(x_i;w^*))$
- 令$f_t=\rho^*h_t(x;w^*)$，更新模型
输出$F_t$

稍微总结一下上两节(集成算法和梯度提升决策树)的内容，实际上述两节是一起的，但是内容过多而且非常重要，所以拆成了两节。首先说了两种最重要的集成算法，boosting和bagging。boosting算法的代表有AdaBoost、梯度提升树，有名的工具包如XGBoost, LightGBM等，而bagging算法的代表有随机森林。实际上集成算法还包括stacking和blending等，stacking也是比较常用的集成算法，可参见：详解stacking过程、集成学习中的 stacking 以及python实现。实际上，单是一个详解的boosting算法的篇幅都不止如此，况且并无能力指点江山。这里有篇关于XGBoost比较好的解释并且回答中包含了一个PPT，可以下载下来仔细看看：wepon-机器学习算法中 GBDT 和 XGBOOST 的区别有哪些?

再次强调，这部分非常重要，篇幅不够只是因为理解不深，不敢乱写而已:)

大文件排序

大文件，文件大小远大于内存大小，文件为若干数字，要求对这些数字排序

外部排序：内存极少情况下，利用分治策略，利用外存保存中间结果，再用多路归并排序

具体步骤：

1)将大文件根据实际内存大小，分割为合理大小的小文件

2)对每个小文件利用内部排序进行排序

3)每次利用胜者树拿到各个小文件的最小值，从而得到全局最小值，每次将全局最小值写入最终的结果大文件

总而言之，分治和合并的过程。

胜者树和败者树可以在$log(n)$的时间内找到最值。胜者树的叶节点存储实际数字，非叶节点存储“胜者”下标。参见：胜者树与败者树

Word2Vec

模型无法直接处理文字，需要转化为实数向量的形式。将word映射到一个新的空间中，并以多维的连续实数空间向量进行表示，叫做word representation，或者word embedding。word embedding目前可以划分为两种方法。一是稀疏表示，如词袋等。二是非稀疏表示，如Word2Vec。Word2Vec在转化后的向量维度大幅降低，且能“保持词语语义”。举例而言，希望将"queen"转化为向量形式，使用one-hot表示，可能需要10000维向量，而使用Word2Vec表示，可能只要20维向量；Word2Vec还能保持词语的含义，两个词转化后的向量距离越小，其词义越相近。

先导知识:

1)稀疏表示的代表：词袋(one-hot)

假设对于一个文本，将其仅仅看作是一个词集合，而忽略其词序和语法

假设通过语料库训练得到了一个词典：{'hello','world','my'}

则
\[
"world"\to[0,1,0]\\
"my"\to[0,0,1]
\]
这是一个很简单的例子，通过语料库训练到的词典有可能含有10000个词语，这是很常见的:)，那么每个词语转化后的向量维数都为10000维

2)n-gram

n-gram是一种统计语言模型。根据前$n-1$个item预测第$n$个item，这些item可以是音素（语言识别应用），字符（输入法应用），词（分词应用）。一般可以从大规模文本或者语料库中生成n-gram模型。

从字符层级上看，给定一串字符，如for ex_，n-gram可以用来预测下一个可能的字符

假设T是由词序列$A_1,A_2,....A_n$组成，则
\[
p(T)=p(A_1,A_2,...,A_n)=p(A_1)p(A_2|A_1)p(A_3|A_1,A_2)...p(A_n|A_1,A_2,...,A_{(n-1)})
\]
其实就是马尔科夫假设：一个item出现的概率只与前m个item有关

参见词袋模型的通俗介绍

Word2Vec

分为两种语言模型：CBOW和Skip-gram
CBOW根据上下文的词语预测当前词语出现概率
- 最大化对数似然函数$L=\sum _{w\in c}log\ P(w|context(w))$
- 输入层是上下文的词向量（词向量是CBOW的参数，实际上是CBOW的副产物）
- 投影层是简单的向量加法
- 输出层是输出最可能的w。由于词料库中词汇量是固定的|c|个，可以将其看作是多分类问题。最后一层是Hierarchical softmax:
  \[
  p(w|context(w))=\prod_{j=2}^{l^w}p(d_j^w|x_w,\theta_{j-1}^w)
  \]
  
  从根节点到叶节点经过了$l^{w}-1$个节点，编码从下标2开始（根节点无编码），对应的参数向量下标从1开始。
skip-gram 已知当前词语，预测上下文
- 与CBOW不同之处在于：
  1. 输入层不再是多个词向量，而是一个词向量
  2. 投影层实际什么都没干，直接将输入层的词向量传递给输出层
- 模型：
  \[
  p(context(w)|w)= \prod_{w \in context(w)}p(u|w)
  \]
- 这是一个词袋模型，所以每个u都是无序，相互独立的
Doc2Vec

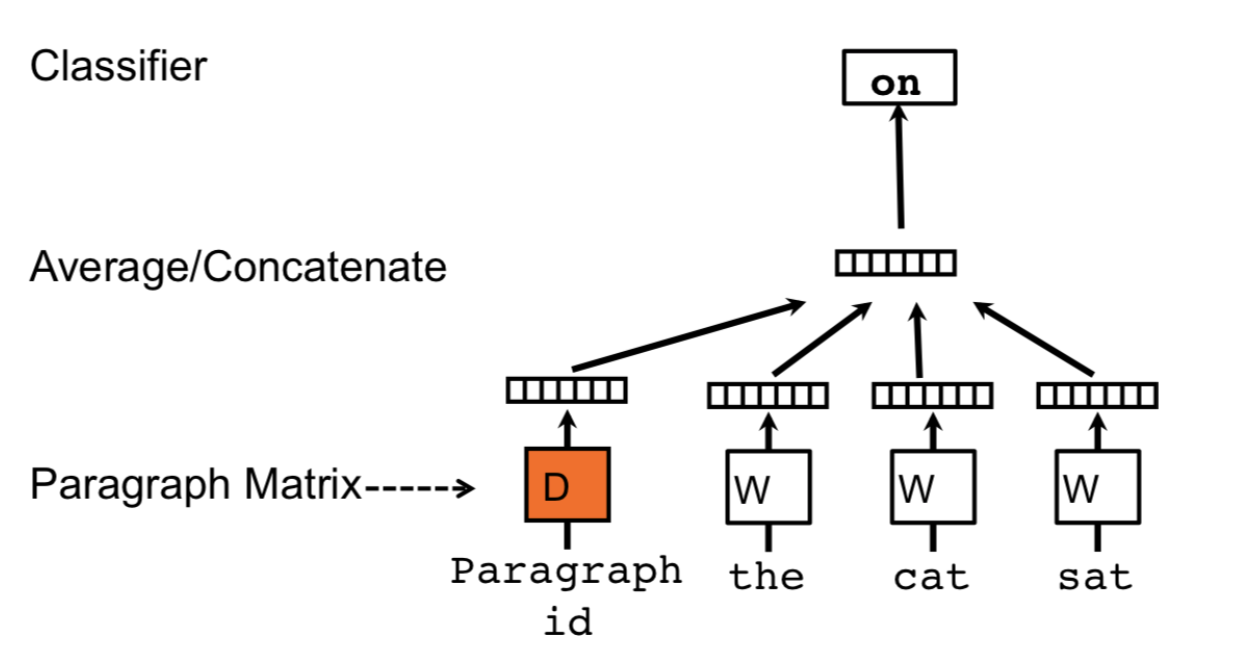
与Word2Vec唯一不同之处在于，串联起word vector在上下文中预测下一个单词。

上下文是固定长度且在段落中sliding window中采样，段落向量在一段中共享在同一段中产生的所有窗口，但是不同段间不共享。

Connect

Email: cncmn@sina.cn

GitHub: cnlinxi@github

后记

这本是开学初整理的一份笔记，是当时感兴趣的点写写记记而成。本文只是介绍了机器学习领域非常小的一部分，权当管中窥豹。实际上这篇又是拾人牙慧，我尽可能在记得的地方加以引用，但难免疏漏，还请告知以补上引用。以及这里面肯定夹带了我的私货，如有错误，还请斧正。

周志华-《机器学习》

李航-《统计学习方法》