UVALive - 5695 The Last Puzzle (思维+区间dp)

题目链接

题目大意：有n个按钮排成一条直线，你的任务是通过左右移动按下所有按钮，按钮如果一段时间没有被按下就会被弹开。

以下是我的推论（不一定正确）：

直观地看的话，如果选择的是最优路径，那么路径的形状必然是若干条区域逐渐缩小的折线，如图所示：

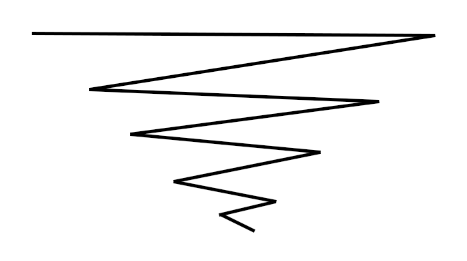
而不可能出现这个样子：

因为，如果这样走的话，那么中间从A到B一段反复经过的区域就全都浪费了，不如直接从C走到D划算。

进一步观察可以发现，每一个按钮只有最后一次被按下的时候是有效的，因此答案序列应当是一个从两边向中间聚合的过程。

设dp[L][R][f]表示当前在区间[L,R]的左端点(f=0)或右端点(f=1)，将区间[L,R]中的所有按钮全部按下所需的最短时间，每一步只有两种选择：

1.按下当前按钮并往前走一步，以后就都不管这个按钮了，此时$dp[L][R][0]=min(dp[L][R][0],dp[L+1][R][0])+dis[L+1]-dis[L]) $(以左端点为例，右端点类似，下同。dis[i]表示i点与左端点的距离)

2.跑到对面去准备按下对面的按钮，此时$dp[L][R][0]=min(dp[L][R][0],dp[L][R][1])+dis[R]-dis[L]) $

总复杂度$O(n^2)$

吐槽：ZOJ凉了，HDU后台有问题过不了，只能交到UVAlive上了，QAQ

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int N=+,inf=0x3f3f3f3f;
 int dp[N][N][],op[N][N][],n,t[N],dis[N];
 int dfs(int L,int R,int f) {
     int& ret=dp[L][R][f],&opp=op[L][R][f];
     if(~ret)return ret;
     if(L==R)return ret=;
     ret=inf;
     if(f==) {
         int x=dfs(L+,R,)+dis[L+]-dis[L];
         int y=dfs(L,R,)+dis[R]-dis[L];
         if(x<t[L]&&x<ret)ret=x,opp=;
         if(y<ret)ret=y,opp=;
     } else {
         int x=dfs(L,R-,)+dis[R]-dis[R-];
         int y=dfs(L,R,)+dis[R]-dis[L];
         if(x<t[R]&&x<ret)ret=x,opp=;
         if(y<ret)ret=y,opp=;
     }
     return ret;
 }
 vector<int> ans;
 void pr(int L,int R,int f) {
     if(L==R) {ans.push_back(L); return;}
     int opp=op[L][R][f];
     if(opp==) {
         if(f==)ans.push_back(L),pr(L+,R,f);
         else ans.push_back(R),pr(L,R-,f);
     } else pr(L,R,f^);
 }
 int main() {
     while(scanf("%d",&n)==) {
         for(int i=; i<=n; ++i)scanf("%d",&t[i]);
         for(int i=; i<=n; ++i)scanf("%d",&dis[i]);
         memset(dp,-,sizeof dp);
         int x=dfs(,n,),y=dfs(,n,);
         if(x==inf&&y==inf)puts("Mission Impossible");
         else {
             ans.clear();
             if(x<=y)pr(,n,);
             else pr(,n,);
             for(int i=; i<ans.size(); ++i)printf("%d%c",ans[i]," \n"[i==ans.size()-]);
         }
     }
     return ;
 }