斐波那契数列F(n)【n超大时的（矩阵加速运算） 模板】

hihocoder #1143 : 骨牌覆盖问题·一

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

骨牌，一种古老的玩具。今天我们要研究的是骨牌的覆盖问题：
我们有一个2xN的长条形棋盘，然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘，一共有多少种不同的覆盖方法呢？
举个例子，对于长度为1到3的棋盘，我们有下面几种覆盖方式：

提示：骨牌覆盖

提示：如何快速计算结果

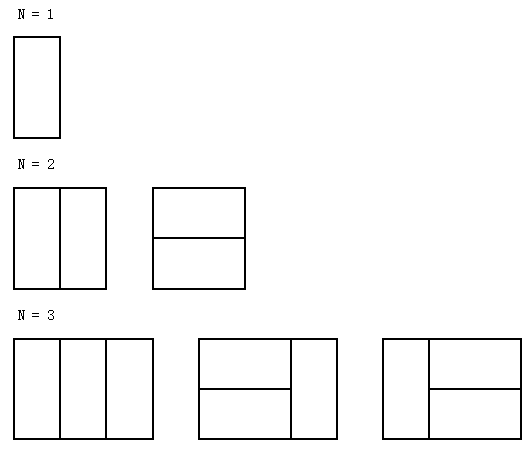
输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 19999997

样例输入

62247088

样例输出

17748018

分析：n超大，如果按照递推计算斐波那契第n项相当费时间，线性代数的矩阵有加速运算的效果。

此代码基本可以算作模板，但需要注意一个地方，在上面的这道题目中，f[1]=1,f[2]=2,,,以此类推下去。
但有的序列可能是：1 1 2 3，，，因为有一点不同就需要稍微修改一下矩阵累乘的次数，也就是矩阵的指数。
代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
#include <string>
#include <vector>
#include <queue>
#include <math.h>
#define eps 1e-8
#include <algorithm>

using namespace std;

//矩阵快速幂运算(矩阵加速运算)

struct matrix{
    long long a[2][2]; //定义2x2的矩阵
};

matrix mul(matrix x, matrix y, long mod )
{
    matrix ret; //按照矩阵相乘求ret矩阵的每个元素的值 然后返回它
    ret.a[0][0]=((x.a[0][0]%mod)*y.a[0][0]%mod + (x.a[0][1]%mod)*y.a[1][0]%mod )%mod;
    ret.a[0][1]=((x.a[0][0]%mod)*y.a[0][1]%mod + (x.a[0][1]%mod)*y.a[1][1]%mod )%mod;
    ret.a[1][0]=((x.a[1][0]%mod)*y.a[0][0]%mod + (x.a[1][1]%mod)*y.a[1][0]%mod )%mod;
    ret.a[1][1]=((x.a[1][0]%mod)*y.a[0][1]%mod + (x.a[1][1]%mod)*y.a[1][1]%mod )%mod;
    return ret;
}

//求矩阵x的幂取模，e为指数
matrix mypow(matrix x, long long e, long mod)//(x^e)%mod
{
    matrix ret, temp;
    if(e==0){
        ret.a[0][0]=1; ret.a[0][1]=0;
        ret.a[1][0]=0; ret.a[1][1]=1;
        return ret;
    }
    if(e==1) return x; //当指数为1时，返回原来的矩阵

    temp=mypow(x, e>>1, mod); //x的 e/2次方
    ret=mul(temp, temp, mod); //ret=temp*temp
    if(e&1) ret=mul(ret, x, mod); //如果e为奇数，ret乘以x

    return ret; //返回答案
}

int main()
{
    long n, m=19999997;//m就是mod
    matrix ans;

    while(scanf("%ld", &n)!=EOF)
    {
        //矩阵初始化
        ans.a[0][0]=1; ans.a[0][1]=1;
        ans.a[1][0]=1; ans.a[1][1]=0;

        if( n ){
            ans = mypow(ans, n, m); //此处的n就是指数（考虑n是否在对应的题目中需要修改）， m是取模数
            printf("%lld\n", ans.a[0][0]);
        }else{
            printf("0\n");
        }
    }
    return 0;
}