CodeForces 909E Coprocessor(无脑拓扑排序)

You are given a program you want to execute as a set of tasks organized in a dependency graph. The dependency graph is a directed acyclic graph: each task can depend on results of one or several other tasks, and there are no directed circular dependencies between tasks. A task can only be executed if all tasks it depends on have already completed.

Some of the tasks in the graph can only be executed on a coprocessor, and the rest can only be executed on the main processor. In one coprocessor call you can send it a set of tasks which can only be executed on it. For each task of the set, all tasks on which it depends must be either already completed or be included in the set. The main processor starts the program execution and gets the results of tasks executed on the coprocessor automatically.

Find the minimal number of coprocessor calls which are necessary to execute the given program.

Input

The first line contains two space-separated integers N (1 ≤ N ≤ 105) — the total number of tasks given, and M (0 ≤ M ≤ 105) — the total number of dependencies between tasks.

The next line contains N space-separated integers 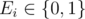. If Ei = 0, task i can only be executed on the main processor, otherwise it can only be executed on the coprocessor.

The next M lines describe the dependencies between tasks. Each line contains two space-separated integers T1 and T2 and means that task T1 depends on task T2 (T1 ≠ T2). Tasks are indexed from 0 to N - 1. All M pairs (T1, T2) are distinct. It is guaranteed that there are no circular dependencies between tasks.

Output

Output one line containing an integer — the minimal number of coprocessor calls necessary to execute the program.

Examples

input

Copy

4 3
0 1 0 1
0 1
1 2
2 3

output

Copy

2

input

Copy

4 3
1 1 1 0
0 1
0 2
3 0

output

Copy

1

Note

In the first test, tasks 1 and 3 can only be executed on the coprocessor. The dependency graph is linear, so the tasks must be executed in order 3 -> 2 -> 1 -> 0. You have to call coprocessor twice: first you call it for task 3, then you execute task 2 on the main processor, then you call it for for task 1, and finally you execute task 0 on the main processor.

In the second test, tasks 0, 1 and 2 can only be executed on the coprocessor. Tasks 1 and 2 have no dependencies, and task 0 depends on tasks 1 and 2, so all three tasks 0, 1 and 2 can be sent in one coprocessor call. After that task 3 is executed on the main processor.

题意：给你一堆任务，有些要用主处理器处理，有些要用副处理器处理，副处理器可以一次处理很多个任务，一个任务能被执行的条件为前继任务已经被执行过了或者前继任务和自己同时被放进副处理器处理，现在给你这些前继任务的关系和每个任务处理要用的处理器，求副处理器最少运行了几次，保证关系是一张有向无环图

题解：

用贪心的思想，每次把所有当前能做得要用主处理器的任务都做光，那么此时能一锅端的副处理器任务肯定也是最多的。所以首先建两个队列，一个放拓扑排序搜到的要用主处理器做得任务，一个放副处理器做的任务，每次先拓扑排序搜到没有能用主处理器做的任务为止，然后如果副处理器的队列里还有别的数，那么ans++，把副处理器队列里的数继续拿出来进行拓扑排序，直到所有数都被搜过为止，复杂度就是拓扑排序的复杂度，还是很优越的。（恕我直言，这一场简直有毒，ab姑且不讲，c题无脑dp，d题滑稽模拟，e题竟然如此简单……不过f题还是不错的，有d题难度（雾）这不会就是传说中的div3吧2333）

代码如下：

#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

struct node
{
    int val,du;
} a[];

int n,m,vis[],ans;
vector<int> g[];

int main()
{
    scanf("%d %d",&n,&m);
    for(int i=; i<=n; i++)
    {
        scanf("%d",&a[i].val);
    }
    for(int i=; i<=m; i++)
    {
        int from,to;
        scanf("%d%d",&from,&to);
        g[to+].push_back(from+);
        a[from+].du++;
    }
    queue<int> q[];
    for(int i=; i<=n; i++)
    {
        if(!a[i].du)
        {
            q[a[i].val].push(i);
        }
    }
    while((!q[].empty())||(!q[].empty()))
    {
        while(!q[].empty())
        {
            int u=q[].front();
            vis[u]=;
            q[].pop();
            for(int i=; i<g[u].size(); i++)
            {
                if(!vis[g[u][i]])
                {
                    a[g[u][i]].du--;
                    if(!a[g[u][i]].du)
                    {
                        q[a[g[u][i]].val].push(g[u][i]);
                    }
                }
            }
        }
        if(!q[].empty())
        {
            ans++;
            while(!q[].empty())
            {
                int u=q[].front();
                vis[u]=;
                q[].pop();
                for(int i=; i<g[u].size(); i++)
                {
                    if(!vis[g[u][i]])
                    {
                        a[g[u][i]].du--;
                        if(!a[g[u][i]].du)
                        {
                            q[a[g[u][i]].val].push(g[u][i]);
                        }
                    }
                }
            }
        }
    }
    printf("%d\n",ans);
}