Batch训练的反向传播过程

Batch训练的反向传播过程

本文试图通过Softmax理解Batch训练的反向传播过程

采用的网络包含一层全连接和一层softmax，具体网络如下图所示:

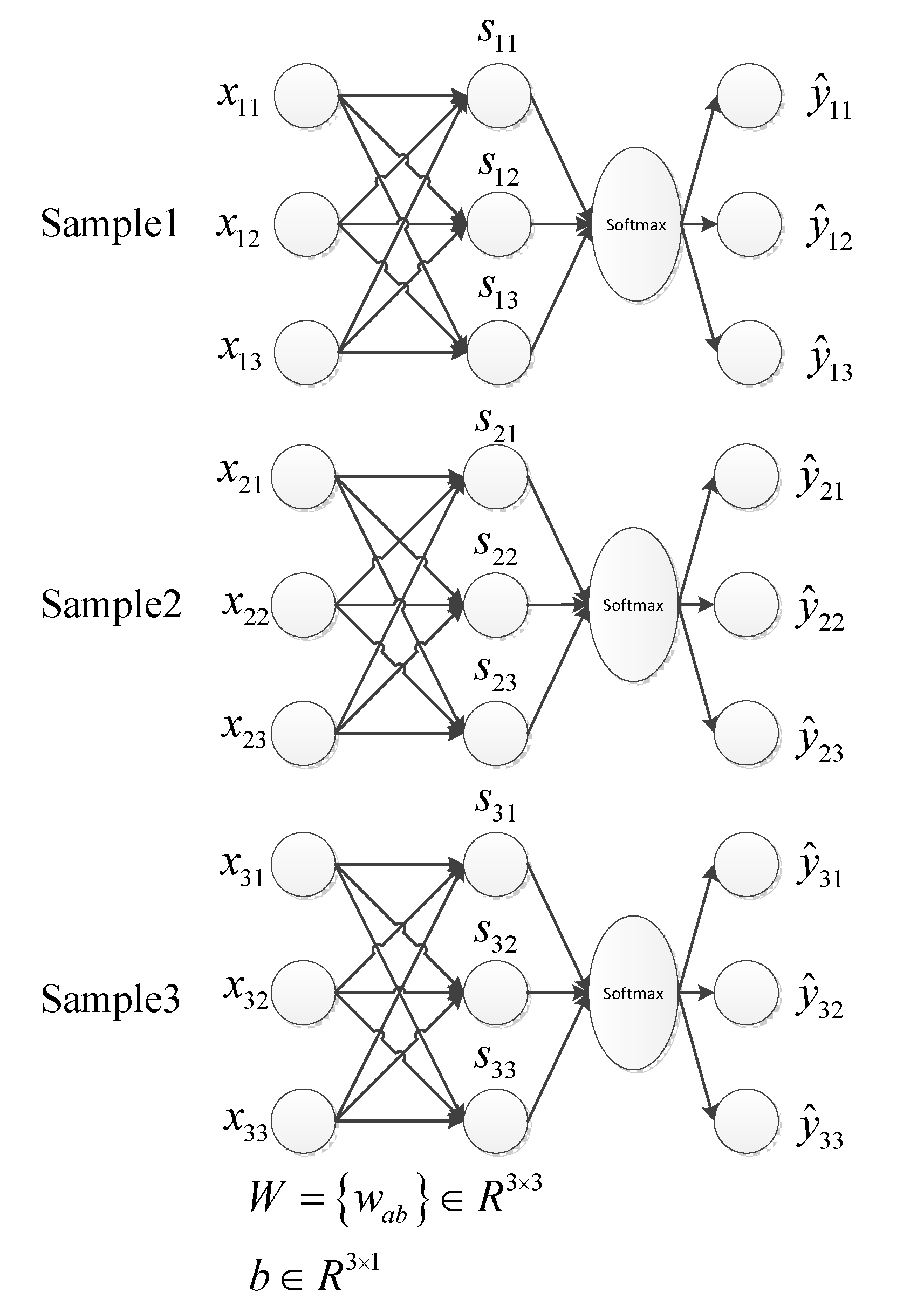
交叉熵成本函数: \[L = - \frac{1}{m}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^N {{y_{ij}}\log {{\hat y}_{ij}}} }.\]

where \(m\) is the number of sample, \(N\) denotes the number of class, \({{\hat y}_{ij}} = \frac{{{e^{{s_{ij}}}}}}{{\sum\limits_j {{e^{{s_{ij}}}}} }}\) is the ouput of softmax, \(y_{ij}\) is the lable for sample \(i\).

当假设3个Sample的样本label均为\([1,0,0]^\rm{T}\)时，上式可简化为：

\[L = - \frac{1}{m}\sum\limits_{i = 1}^m {{y_{i1}}\log {{\hat y}_{i1}}}, \]

Softmax层反向传播： \[\frac{{\partial L}}{{\partial {s_{i1}}}} = {{\hat y}_{i1}} - 1,i\in\{1,\cdots,m\},\]

\[\frac{{\partial L}}{{\partial {s_{ij}}}} = {{\hat y}_{ij}}(j \ne 1),i\in\{1,\cdots,m\}.\]

全连接层反向传播：

\[ \begin{array}{l} \frac{{\partial L}}{{\partial {w_{a1}}}} = \sum\limits_{i = 1}^m {\left( {\frac{{\partial L}}{{\partial {s_{i1}}}}\frac{{\partial {s_{i1}}}}{{\partial {w_{a1}}}}} \right)} = \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{{\hat y}_{i1}} - 1} \right){x_{ia}}} \\ \frac{{\partial L}}{{\partial {w_{a2}}}} = \sum\limits_{i = 1}^m {\left( {\frac{{\partial L}}{{\partial {s_{i2}}}}\frac{{\partial {s_{i2}}}}{{\partial {w_{a2}}}}} \right)} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\hat y}_{i2}}{x_{ia}}} \\ \frac{{\partial L}}{{\partial {w_{a3}}}} = \sum\limits_{i = 1}^m {\left( {\frac{{\partial L}}{{\partial {s_{i3}}}}\frac{{\partial {s_{i3}}}}{{\partial {w_{a3}}}}} \right)} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\hat y}_{i3}}{x_{ia}}} \\ \frac{{\partial L}}{{\partial {b_{a1}}}} = \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{{\hat y}_{i1}} - 1} \right)} \\ \frac{{\partial L}}{{\partial {b_{a2}}}} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\hat y}_{i2}}} \\ \frac{{\partial L}}{{\partial {b_{a3}}}} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\hat y}_{i3}}} \end{array} \]