Dijkstra【迪杰斯特拉算法】

有关最短路径的最后一个算法——Dijkstra

迪杰斯特拉算法是由荷兰计算机科学家迪杰斯特拉于1959 年提出的，因此又叫迪杰斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

本蒟蒻认为这个是最为重要的一个有关最短路径的算法

　　Dijkstra使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。

　　它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

　　它主要采用的是一种贪心的策略，声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合：T，初始时，原点 s 的路径权重被赋为 0 （dis[s] = 0）。若对于顶点 s 存在能直接到达的边（s,m），则把dis[m]设为w（s, m）,同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大。初始时，集合T只有顶点s。
然后，从dis数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入到T中，OK，此时完成一个顶点，
　　然后，我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在dis中的值。
　　最后，又从dis中找出最小值，重复上述动作，直到T中包含了图的所有顶点。

下面用以为大佬的图来举个例子

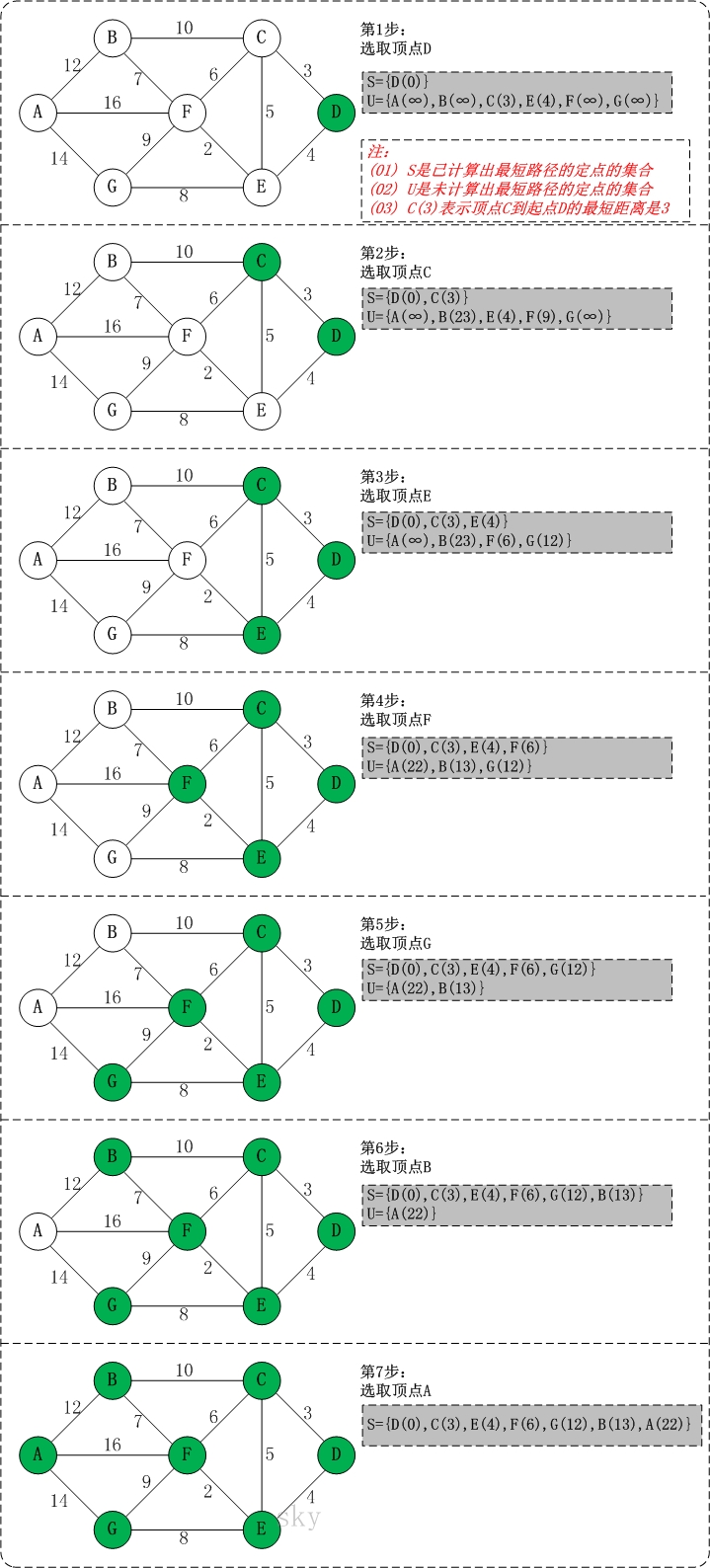
首先是相对来说较容易理解的代码

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
    int X=,w=;
    char c=getchar();
    while(c<''||c>'')
    {
        if (c=='-')
        {
            w=-;
            c=getchar();
        }
    }
    while(c>=''&&c<='')
    {
        X=(X<<)+(X<<)+c-'';
        c=getchar();
    }
    return X*w;
}
const int maxn=;
int g[maxn][maxn];//g数组用来存储图;
int n,m,s;//分别表示点的个数、有向边的个数、出发点的编号;
bool vis[maxn];//表示是否已经到达过;
int d[maxn];//d[i]表示从询问点到点i的最短路径;
const int inf=;
int main ()
{
    n=read(),m=read(),s=read();
    for(int i=;i<=n;i++)
    {
        d[i]=inf;
        for(int j=;j<=n;j++)
            g[i][j]=inf;
        g[i][i]=;//自己到自己的最短路径当然是0
    }//初始化数组;
    for(int i=;i<=m;i++)
    {
        int u=read(),v=read(),w=read();
        //u,v,i分别表示第i条有向边的出发点、目标点和长度;
        g[u][v]=w;//读入;
    }
    vis[s]=;//将起点标记成已经到达;
    for(int i=;i<=n;i++)
        d[i]=g[s][i];//将最短路径初始化;
        //如果两点之间有路线就初始化为该距离，如果没有就还是inf;
    while()
    {
        int stt_node=,stt_dis=inf;//stt=shortest 初始化两个变量
        // stt_node表示最短路径的终点，stt_dis表示最短路径的长度
        for(int i=;i<=n;i++)
        {
            if(vis[i]==&&d[i]<stt_dis)
            //如果该点还没有到达，并且他的距离小于最短距离
            {
                stt_node=i,stt_dis=d[i];//更新变量
            }
        }
        if(stt_node==) break;
        //如果已经没有可以更新的最短路径了，就说明已经结束了
        vis[stt_node]=;//将该点标记成已经到达
        for(int i=;i<=n;i++)
        {
            if(vis[i]||g[stt_node][i]==inf)continue;
            //如果并没有到达或者是两点之间没有路径，就跳出循环
            d[i]=min(d[i],stt_dis+g[stt_node][i]);//更新最短路径
        }
    }
    for(int i=;i<=n;i++)
        printf("%d ",d[i]);
    return ;
}

下面便是代码实现了qwq：

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int nmax=,mmax=;
int fir[nmax],to[mmax],nxt[mmax],dis[mmax],ecnt;
void add(int u,int v,int w)
{
    to[++ecnt]=v;
    dis[ecnt]=w;
    nxt[ecnt]=fir[u];
    fir[u]=ecnt;
}
struct node
{
    int x,d;
    node(int x,int d):x(x),d(d){}
};
bool operator<(node a,node b)
{
    return a.d>b.d;
}
int d[nmax];
bool vis[nmax];
void dijkstra(int s)
{
    memset(vis,,sizeof(vis));
    memset(d,-,sizeof(d));
    priority_queue<node>q;
    q.push(node(s,));
    d[s]=;
    while(!q.empty())
    {
        node h=q.top();
        q.pop();
        if(vis[h.x])continue;
        vis[h.x]=;
        for(int e=fir[h.x];e;e=nxt[e])
        {
            if(vis[to[e]])continue;
            if(d[to[e]]==-)
            {
                d[to[e]]=h.d+dis[e];
            }
            else
            {
                d[to[e]]=min(d[to[e]],h.d+dis[e]);
            }
            vis[to[e]]=;
            q.push(node(to[e],d[to[e]]));
        }
    }
}
int main()
{
    cin>>n>>m;
    for(int i=;i<=m;i++)
    {
        int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
        add(v,u,w);
    }
    dijkstra();
    for(int i=;i<=n;i++)
    {
        cout<<d[i]<<' ';
    }
}