python穷举法解数独

总体思路 ：

数独九行九列，一个list装一行，也就需要一个嵌套两层的list

初始会有很多数字，我可不想一个一个赋值

那就要想办法偷懒啦

然后再是穷举，如何科学的穷举

第一部分：录入

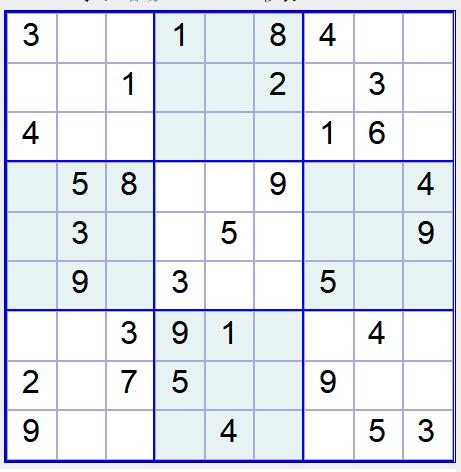
某在线数独网站的截图

要想办法，把它方便的变成嵌套的list

我的解决办法：

手打到Excel里面

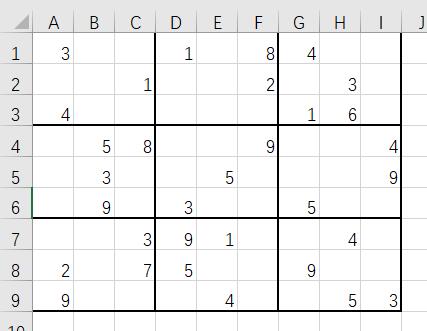
然后另存为csv文件

然后就当做txt读取

l = None
with open('数独.csv','r',encoding = 'utf-8') as f:
    l = f.readlines()

print(l)
'''
运行结果
---------------------------------------
['\ufeff3,,,1,,8,4,,\n', ',,1,,,2,,3,\n', '4,,,,,,1,6,\n', ',5,8,,,9,,,4\n', ',3,,,5,,,,9\n', ',9,,3,,,5,,\n', ',,3,9,1,,,4,\n', '2,,7,5,,,9,,\n', '9,,,,4,,,5,3\n']

'''

发现文本开头有个莫名其妙的\ufeff，另外它的长度是1

>>> s = '\ufeff3'
>>> len(s)
2

只好加一句    l[0] = l[0][1:]

然后去掉末尾的\n 再以逗号为界切割

l = None
with open('数独.csv','r',encoding = 'utf-8') as f:
    l = f.readlines()
    l[0] = l[0][1:]
    l = map(lambda i : i.rstrip(),l)
    l = map(lambda i : i.split(","),l)

for i in l:
    print(i,'---', len(i))
'''
运行结果
---------------------------------------
['3', '', '', '1', '', '8', '4', '', ''] --- 9
['', '', '1', '', '', '2', '', '3', ''] --- 9
['4', '', '', '', '', '', '1', '6', ''] --- 9
['', '5', '8', '', '', '9', '', '', '4'] --- 9
['', '3', '', '', '5', '', '', '', '9'] --- 9
['', '9', '', '3', '', '', '5', '', ''] --- 9
['', '', '3', '9', '1', '', '', '4', ''] --- 9
['2', '', '7', '5', '', '', '9', '', ''] --- 9
['9', '', '', '', '4', '', '', '5', '3'] --- 9
'''

九行九列..完美

下一步全部处理成数字

鉴于int()无法将空字符串转化为0 所以需要新定义一个new_int

def new_int(s):
    return int(s) if s else 0

l = None
with open('数独.csv','r',encoding = 'utf-8') as f:
    l = f.readlines()
l[0] = l[0][1:]
l = map(lambda i : i.rstrip(),l)
l = map(lambda i : i.split(","),l)
l = [ list(map(new_int, i)) for i in l]

for i in l:
    print(i)
'''
运行结果
---------------------------------------
[3, 0, 0, 1, 0, 8, 4, 0, 0]
[0, 0, 1, 0, 0, 2, 0, 3, 0]
[4, 0, 0, 0, 0, 0, 1, 6, 0]
[0, 5, 8, 0, 0, 9, 0, 0, 4]
[0, 3, 0, 0, 5, 0, 0, 0, 9]
[0, 9, 0, 3, 0, 0, 5, 0, 0]
[0, 0, 3, 9, 1, 0, 0, 4, 0]
[2, 0, 7, 5, 0, 0, 9, 0, 0]
[9, 0, 0, 0, 4, 0, 0, 5, 3]
'''

第二部分 穷举

假设81个格子有50是空的，每个格子1-9  9种可能

>>> 9**50
515377520732011331036461129765621272702107522001

显然不能傻乎乎的直接遍历

其实一个新格子并不是1-9 9种可能
它不可能是同行，同列，同区出现过的数字
这里将会用到set的加减

x,y = 0,1
whole = {1,2,3,4,5,6,7,8,9}
x_set = set(l[x])
#行
y_set = { l[i][y] for i in range(9) }
#列
block_num = big_small[(x,y)]
#查字典得到区号
block_set = {  l[i][j] for i , j in small_big[block_num]  }
#根据区号查该区的9个方格,然后根据位置构建set
possible = whole - x_set - y_set - block_set

下面补充下big_small和small_big两个字典

3x3的小区共9个 分别编号上0-8
0 | 1 | 2
3 | 4 | 5
6 | 7 | 8
原来在9x9的 x行y列 对应过去 就会在x//3行y//3列
对应编号就是x//3*3 + y//3

为了方便后面的使用，建立一个字典

big_small = { (x,y): (x//3)*3+(y//3)  for x in range(9) for y in range(9)}
'''
---------------------------
>>> big_small[(5,5)]
4
'''

这个字典是{位置:区号}

然后反着来一下

就可以根据 区号 查包含位置的字典（这才是重点）

big_small = { (x,y): (x//3)*3+(y//3)  for x in range(9) for y in range(9)}

small_big = {  x:[ ]  for x in range(9)}

for i , j in big_small.items():
    small_big[ j ].append(i)

for i,j in small_big.items():
    print(i,'-->',j)
'''
----------------------------------------------------
0 --> [(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)]
1 --> [(0, 3), (0, 4), (0, 5), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)]
2 --> [(0, 6), (0, 7), (0, 8), (1, 6), (1, 7), (1, 8), (2, 6), (2, 7), (2, 8)]
3 --> [(3, 0), (3, 1), (3, 2), (4, 0), (4, 1), (4, 2), (5, 0), (5, 1), (5, 2)]
4 --> [(3, 3), (3, 4), (3, 5), (4, 3), (4, 4), (4, 5), (5, 3), (5, 4), (5, 5)]
5 --> [(3, 6), (3, 7), (3, 8), (4, 6), (4, 7), (4, 8), (5, 6), (5, 7), (5, 8)]
6 --> [(6, 0), (6, 1), (6, 2), (7, 0), (7, 1), (7, 2), (8, 0), (8, 1), (8, 2)]
7 --> [(6, 3), (6, 4), (6, 5), (7, 3), (7, 4), (7, 5), (8, 3), (8, 4), (8, 5)]
8 --> [(6, 6), (6, 7), (6, 8), (7, 6), (7, 7), (7, 8), (8, 6), (8, 7), (8, 8)]
'''

下面列下总体框架(???表示还没确定的细节)

#伪代码
l = ???
#读取文件获得未完成的数独
all_list = [l]
#这个变量用于装 待处理的数独
key_list = []
#装正确的解

while all_list:
    one = all_list.pop()
    #从list末尾取出一个进行处理
    x, y, ed = ???(one)
    #这个函数找一个未填写的格子(值为0)
    #x,y将接受格子的位置,
    #ed接受一个逻辑值,以处理格子全被填满的特殊情况
    if ed :
        key_list.append(one)
        for i in one:
            print(i)
        #输出,保存解
        continue
    possible = ???(x,y,one)
    #获取格子可能的数字
    for i in possible:
        new_one = copy.deepcopy(one)
        #深度拷贝one
        new_one[x][y] = i
        all_list.append(new_one)
        #修改副本,并加入待处理list

只有一个函数不够清晰,

def output_cell(l):
    for i in range(9):
        for j in range(9):
            if l[ i ][ j ] :
                pass
            else:
                return i , j ,False
    else:
        return None, None,True

全部的代码，

import copy

def new_int(s):
    return int(s) if s else 0

def output_cell(l):
    for i in range(9):
        for j in range(9):
            if l[ i ][ j ] :
                pass
            else:
                return i , j ,False
    else:
        return None, None,True

def possible_num(x,y,l):
    whole = {1,2,3,4,5,6,7,8,9}
    x_set = set(l[x])
    y_set = { l[i][y] for i in range(9) }
    block_num = big_small[(x,y)]
    block_set = {  l[i][j] for i , j in small_big[block_num]  }
    possible = whole - x_set - y_set - block_set
    return possible

big_small = { (x,y): (x//3)*3+(y//3)  for x in range(9) for y in range(9)}

small_big = {  x:[ ]  for x in range(9)}

for i , j in big_small.items():
    small_big[ j ].append(i)

l = None
with open('数独.csv','r',encoding = 'utf-8') as f:
    l = f.readlines()
l[0] = l[0][1:]
l = map(lambda i : i.rstrip(),l)
l = map(lambda i : i.split(","),l)
l = [ list(map(new_int, i)) for i in l]

all_list = [l]
key_list = []

while all_list:
    one = all_list.pop()
    x, y, ed = output_cell(one)
    if ed :
        key_list.append(one)
        for i in one:
            print(i)
        continue
    possible = possible_num(x,y,one)
    for i in possible:
        new_one = copy.deepcopy(one)
        new_one[x][y] = i
        all_list.append(new_one)
else:
    print('遍历结束')
print(len_num)

运行结果

'''
---------------------------
[3, 7, 5, 1, 6, 8, 4, 9, 2]
[8, 6, 1, 4, 9, 2, 7, 3, 5]
[4, 2, 9, 7, 3, 5, 1, 6, 8]
[1, 5, 8, 6, 2, 9, 3, 7, 4]
[7, 3, 4, 8, 5, 1, 6, 2, 9]
[6, 9, 2, 3, 7, 4, 5, 8, 1]
[5, 8, 3, 9, 1, 6, 2, 4, 7]
[2, 4, 7, 5, 8, 3, 9, 1, 6]
[9, 1, 6, 2, 4, 7, 8, 5, 3]
'''

#