洛谷 P1027 【Car的旅行路线】

题目描述

又到暑假了，住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场，分别位于一个矩形的四个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第i个城市中高速铁路的单位里程价格为Ti，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为t。

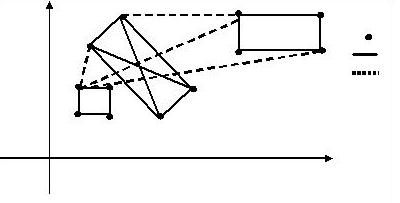
图例（从上而下）

机场 高速铁路 飞机航线

注意：图中并没有标出所有的铁路与航线。

那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题，于是她来向你请教。

找出一条从城市A到B的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

输入

第一行为一个正整数n(0<=n<=10)，表示有n组测试数据。

每组的第一行有四个正整数s，t，A，B。

S(0<S<=100)表示城市的个数，t表示飞机单位里程的价格，A，B分别为城市A，B的序号，(1<=A，B<=S)。

接下来有S行，其中第I行均有7个正整数xi1，yi1，xi2，yi2，xi3，yi3，Ti，这当中的(xi1，yi1)，(xi2，yi2)，(xi3，yi3)分别是第I个城市中任意三个机场的坐标，T I为第I个城市高速铁路单位里程的价格。

输出

共有n行，每行一个数据对应测试数据。保留一位小数。

样例输入

1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3

样例输出

47.5

来源

NOIP2001提高组

本题我们不妨把每个城市的4个机场看做四个点。那样这图就有4×s个点。

根据题目描述，我们又知道：每一个机场都与另外每一个机场互通，差别只是在是否是同一个城市：

如果是，那么只能走高速铁路；

如果不是，那么只能走航道。用一个判断来计算这条路的花费即可。

最后跑最短路，答案为到达城市的4个机场的花费的最小值。

（因为有几行太长了，另一种着色方法的代码格式会乱，只好用这种了【手动滑稽】）

#include <cstdio>
#include <cmath>
#include <cstring>
#include <queue>
using namespace std;

struct data {
    int x,y; //(x,y)
    int city; // 所在城市
};

const int maxn=100;
int s,t,A,B;
int T[maxn+1];
double dis[maxn<<2|1];
data a[maxn<<2|1];

int pingfang(int x) { return x*x; }

//两点间距离公式
double juli(int x1, int y1, int x2, int y2) { return sqrt(pingfang(x1-y1)+pingfang(x2-y2)); }

//求矩形的第四个点的函数
void get_4th(int x1, int y1, int x2, int y2, int x3, int y3, int i) {
    //已知A(x1,y1),B(x2,y2),C(x3,y3)，求D(x4,y4)
    //ab表示AB^2,ac表示AC^2,BC表示BC^2
    int ab=pingfang(x1-x2)+pingfang(y1-y2),
        ac=pingfang(x1-x3)+pingfang(y1-y3),
        bc=pingfang(x2-x3)+pingfang(y2-y3);
    int x4,y4;
    //用勾股定理的逆定理，判断谁是直角边
    //再根据矩形对边平行的性质，算出第四个点的坐标
    if (ab+ac==bc) x4=x2+x3-x1, y4=y2+y3-y1;
    if (ab+bc==ac) x4=x1+x3-x2, y4=y1+y3-y2;
    if (ac+bc==ab) x4=x1+x2-x3, y4=y1+y2-y3;
    a[i+3].x=x4;
    a[i+3].y=y4;
}

//初始化函数如题意所述
void init() {
    memset(a,0,sizeof(a));
    scanf("%d%d%d%d",&s,&t,&A,&B);
    //对每个城市的机场进行处理
    for (int i=1; i<=4*s; i+=4) {
        scanf("%d%d%d%d%d%d%d",&a[i].x,&a[i].y,&a[i+1].x,&a[i+1].y,&a[i+2].x,&a[i+2].y,&T[i/4+1]);
        a[i].city=a[i+1].city=a[i+2].city=a[i+3].city=i/4+1;
        //调用求出第四个点坐标的函数
        get_4th(a[i].x,a[i].y,a[i+1].x,a[i+1].y,a[i+2].x,a[i+2].y,i);
    }
}

//最短路spfa
void spfa() {
    //队内有没有该元素（用于加速）
    bool mark[maxn<<2|1];
    queue <int> q;
    for (int i=1; i<=4*s; i++) dis[i]=99999999.99999;
    //可以从出发地任意一个机场出发，所以初始化都入队，并且花费均为0
    for (int i=A*4-3;i<=A*4;i++)
        dis[i]=0, q.push(i), mark[i]=true;

    //bfs
    while (!q.empty()) {
        int x=q.front(); q.pop(); mark[x]=false;
        //这个机场与其余所有机场都有通路
        for (int i=1; i<=4*s; i++) {
            if (i==x) continue;
            //花费先赋值为两点间的距离
            double cost=juli(a[x].x,a[i].x,a[x].y,a[i].y);
            //如果两机场在同一城市，则走该城市的高速铁路
            if (a[i].city==a[x].city) cost*=T[a[i].city];
            //否则坐飞机
            else cost*=t;
            //如果花费更少则更新
            if (dis[x]+cost<dis[i]) {
                dis[i]=dis[x]+cost;
                if (!mark[i])
                    mark[i]=true, q.push(i);
            }
        }
    }
}

int main() {
    int n;
    scanf("%d",&n);

    //有多组数据
    while (n--) {
        init();
        spfa();
        //答案是到达地四个机场中花费最少的那个
        //用“打擂台”的方法求出最小值
        double ans=dis[B*4];
        for (int i=B*4-3; i<B*4; i++)
            if (dis[i]<ans) ans=dis[i];
        printf("%.1lf",ans);
    }
}