RobotFramework安装扩展库包Selenium2Library（三）

Robot Framework扩展库包

http://robotframework.org/#libraries

一，自动化测试web端

1，pip安装SeleniumLibrary

pip install robotframework-selenium2library

（或者手动安装https://pypi.org/project/robotframework-selenium2library/)

检查一下

pip list

2，下载浏览器驱动,放到C:\Python27目录下

Chrome浏览器驱动

https://github.com/mozilla/geckodriver/releases

（用其他浏览器，自己找驱动下载哈）

3,  运行

》1，双击打开C:\Python27\Scripts目录下的 ride.py

》2，新建个项目，File-->New Project

》3，右键，添加suite，在suite添加库,然后添加Test case

》4，添加library

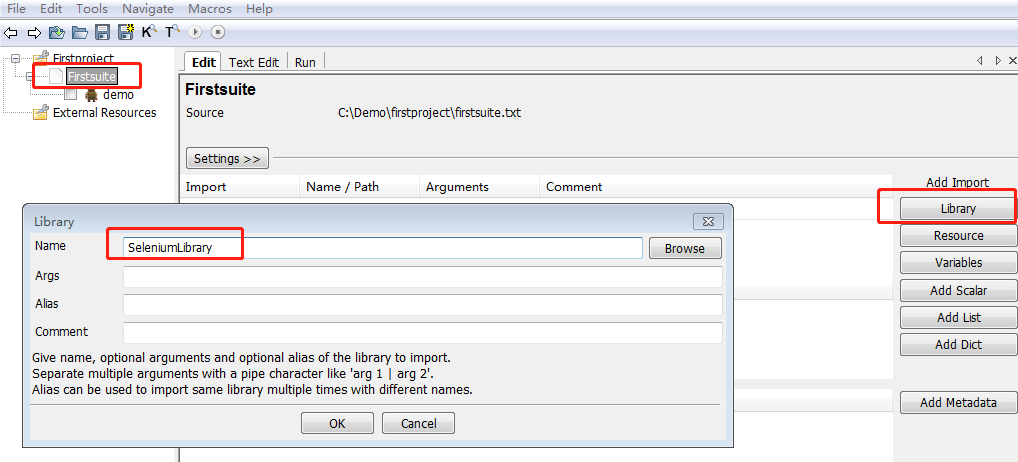
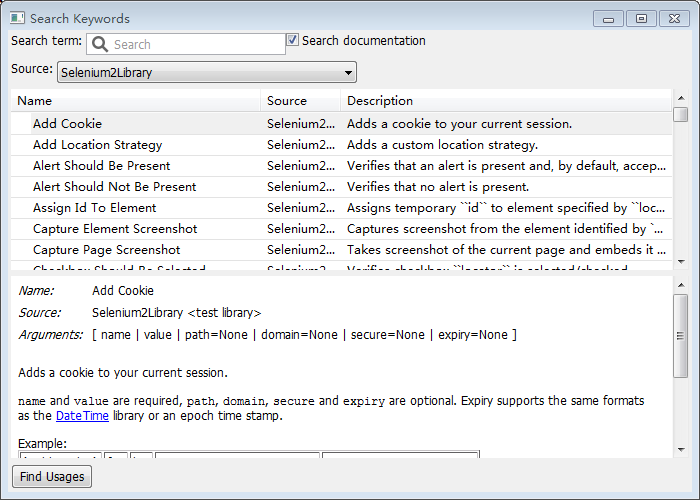
F5 查看 脚本的关键字

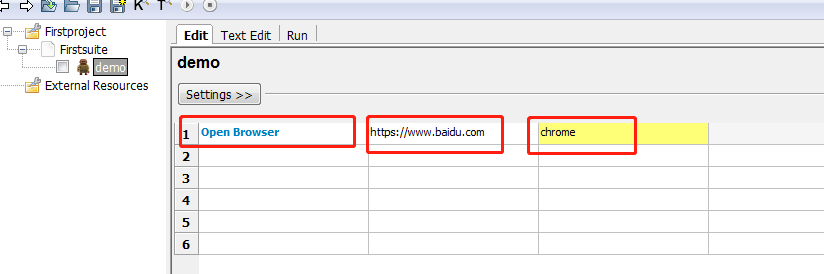
》4，打开谷歌浏览器。哈哈哈。。。。

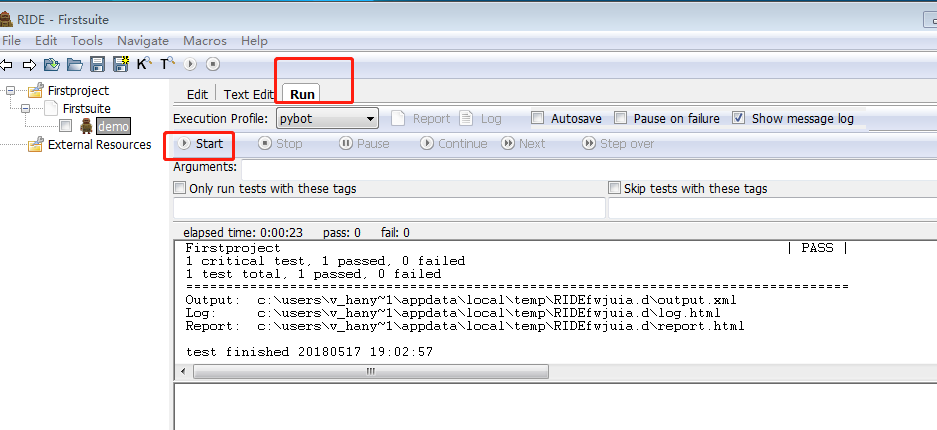
问题：

1，编码问题  UnicodeEncodeError: 'ascii' codec can't encode characters in position 0-1: ordinal not in range(128)

　　在Python目录下的Lib\site-packages文件夹下新建一个sitecustomize.py文件，内容为：

             #coding=utf8
             import sys
             reload(sys)
             sys.setdefaultencoding('utf8')

　　重启

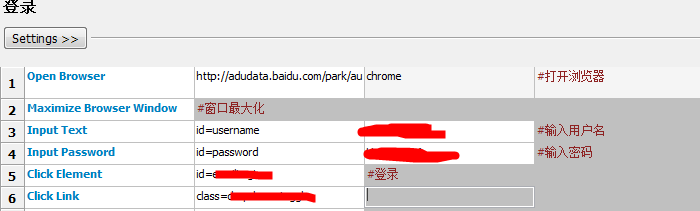
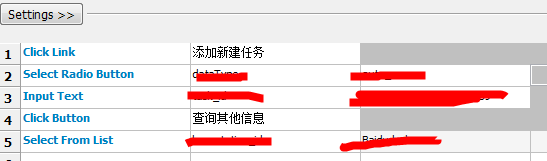
自己工作遇到的查了一些，记录一下，对应的id，在网页 F12 自己找