hdu1876（dp）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1876

题意：问机器人到达终点的过程中最多有几次完全消耗完能量，消耗完这么多次能量的方式有几种。

分析：模拟一下可知，每次走到下一次消耗完时必定在一条对角线上。

以sample为例：

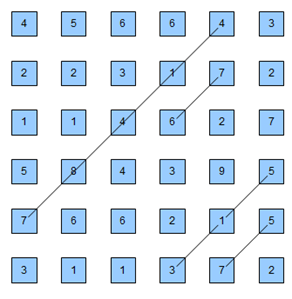
由于整个过程是以对角线的方向递推下去的，每次必定是往右下方走的，所以只需按着正常循环递推即可，当然按对角线右下方循环也可，不过那样略微麻烦。dp[i][j].num表示走到点（i，j）时消最多次耗完能量的次数，dp[i][j].cnt表示走到点（i，j）时消最多次耗完能量的方式。

状态转移方程为：

if(dp[x][y].num<dp[i][j].num+1)
                    {
                        dp[x][y].num=dp[i][j].num+1;
                        dp[x][y].cnt=dp[i][j].cnt;
                    }
                    else if(dp[x][y].num==dp[i][j].num+1)
                        dp[x][y].cnt+=dp[i][j].cnt;

本题还有好几个坑，能量为0的格子不能走，在终点时就不用递推了，样例没有刚好在终点时消耗完能量，所以这里被坑得好惨T^^T

#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cstdlib>
#include <vector>
#include <set>
#include <map>
#define LL long long
#define mod 1000000007
#define inf 0x3f3f3f3f
#define N 10010
using namespace std;
struct node
{
    int cnt,num;
} dp[][];
int flag[][],a[][];
int main()
{
    int t,n,m,x,y;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        for(int i=; i<=n; i++)
            for(int j=; j<=m; j++)scanf("%d",&a[i][j]);
        memset(flag,,sizeof(flag));
        memset(dp,,sizeof(dp));
        flag[][]=;
        dp[][].cnt=;
        for(int i=; i<=n; i++)
            for(int j=; j<=m; j++)
            {
                if(i==n&&j==m)continue;//这里尤为注意
                if(flag[i][j])
                {
                    if(!a[i][j])continue;//能量为0时不能走
                    x=i+a[i][j];
                    y=j;
                    int t=a[i][j]+;
                    if(x+y<=m+n)
                    {
                        while(t--)
                        {
                            if(x>n||y>m||x<=||y<=)//不在方格内不算
                            {
                                x--;
                                y++;
                                continue;
                            }
                            flag[x][y]=;
                            if(dp[x][y].num<dp[i][j].num+)//取次数多的
                            {
                                dp[x][y].num=dp[i][j].num+;
                                dp[x][y].cnt=dp[i][j].cnt;
                            }
                            else if(dp[x][y].num==dp[i][j].num+)
                                dp[x][y].cnt+=dp[i][j].cnt;
                            x--;
                            y++;
                        }
                    }
                    else//走到终点没消耗完能量的
                    {
                        if(dp[n][m].num<dp[i][j].num)
                        {
                            dp[n][m].num=dp[i][j].num;
                            dp[n][m].cnt=dp[i][j].cnt;
                        }
                        else if(dp[n][m].num==dp[i][j].num)
                            dp[n][m].cnt+=dp[i][j].cnt;
                    }
                }
            }
        printf("%d %d\n",dp[n][m].num,dp[n][m].cnt);
    }
}