NOIP 模拟 $11\; \rm biology$

题解

首先对 \(a\) 离散化，则可推出转移方程

\[dp_{i,j}=\max\{{dp_{{i^{'}},{j^{'}}}+|i-i^{'}|+|j-j^{'}|}\}+b_{i,j} \;\;(a_{i,j}=a_{{i^{'}},{j^{'}}}+1)
\]

其中按离散化后 \(a\) 递增 \(1\) 跳，一定为最优（易证）

这个方程复杂度为 \(\mathcal O(n^2m^2)\)，优化：

此题可以发现每个 \(dp_{i,j}\) 都可以由 左上，右上，左下，右下 转移过来。所以用数组维护一下最大值：

\[(1,1)−(i,j):dp_{i,j}−i−j
\]

\[(1,j)−(i,m):dp_{i,j}−i+j
\]

\[(i,1)−(n,j):dp_{i,j}+i−j
\]

\[(i,j)−(n,m):dp_{i,j}+i+j
\]

贴张学长的图

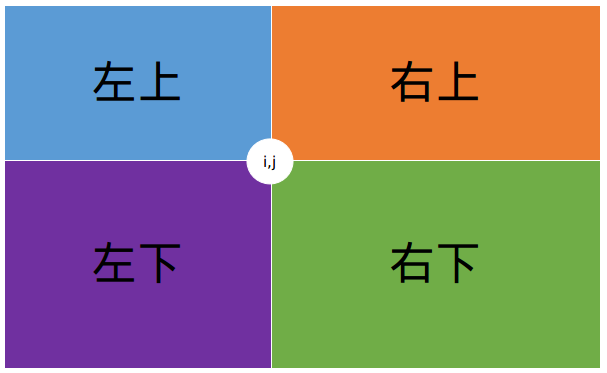
现在证明一下为什么不用判断一个点在另一个点的位置就可以转移

证明：

设贡献点为 \(t_1\)，被转移点为 \(t_2\)

若 \(t_1\) 在 \(t_2\) 左上方，从右下方转移，则 \(dp_{t_{2}}=dp_{t_{1}}-i-j-i'-j'\) ，但若从左上方转移 \(dp_{t_{2}}=dp_{t_{1}}+i+j-i'-j'\)

显然第一种不合法转移会被更优的且合法的第二种转移覆盖，其它情况同理

证毕

Code:

#include<bits/stdc++.h>
#define ri register signed
#define p(i) ++i
using namespace std;
namespace IO{
    char buf[1<<21],*p1=buf,*p2=buf;
    #define gc() p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++
    template<typename T>inline void read(T &x) {
        ri f=1;x=0;register char ch=gc();
        while(ch<'0'||ch>'9') {if (ch=='-') f=0;ch=gc();}
        while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+(ch^48);ch=gc();}
        x=f?x:-x;
    }
}
using IO::read;
namespace nanfeng{
    #define node(x,y,a,b) (node){x,y,a,b}
    #define cmax(x,y) ((x)>(y)?(x):(y))
    #define cmin(x,y) ((x)>(y)?(y):(x))
    #define FI FILE *IN
    #define FO FILE *OUT
    typedef long long ll;
    static const int N=2e3+7;
    int a[N][N],b[N][N],wk[N*N],p[N*N],cnt,n,m;
    ll dp[N*N],pre[4],mx[4];
    struct node{int x,y,a,b;}pnt[N*N];
    inline int cmp(int x,int y) {return pnt[x].a<pnt[y].a;}
    inline int main() {
        // FI=freopen("nanfeng.in","r",stdin);
        // FO=freopen("nanfeng.out","w",stdout);
        read(n),read(m);
        for (ri i(1);i<=n;p(i)) for (ri j(1);j<=m;p(j)) read(a[i][j]);
        for (ri i(1);i<=n;p(i))
            for (ri j(1);j<=m;p(j)) {
                read(b[i][j]);
                if (a[i][j]) p[p(cnt)]=cnt,pnt[cnt]=node(i,j,a[i][j],b[i][j]);
            }
        sort(p+1,p+cnt+1,cmp);
        ri cut=INT_MAX;
        dp[1]=pnt[p[1]].b;
        mx[0]=cmax(mx[0],dp[1]+pnt[p[1]].x+pnt[p[1]].y);
        mx[1]=cmax(mx[1],dp[1]-pnt[p[1]].x+pnt[p[1]].y);
        mx[2]=cmax(mx[2],dp[1]+pnt[p[1]].x-pnt[p[1]].y);
        mx[3]=cmax(mx[3],dp[1]-pnt[p[1]].x-pnt[p[1]].y);
        for (ri i(2);i<=cnt;p(i)) {
            ri x=p[i],y=p[i-1];
            if (pnt[x].a!=pnt[y].a) {cut=i;break;}
            dp[i]=pnt[x].b;
            mx[0]=cmax(mx[0],dp[i]+pnt[x].x+pnt[x].y);
            mx[1]=cmax(mx[1],dp[i]-pnt[x].x+pnt[x].y);
            mx[2]=cmax(mx[2],dp[i]+pnt[x].x-pnt[x].y);
            mx[3]=cmax(mx[3],dp[i]-pnt[x].x-pnt[x].y);
        }
        for (ri i(cut);i<=cnt;p(i)) {
            ri x=p[i],y=p[i-1];
            if (pnt[x].a!=pnt[y].a) {
                pre[0]=mx[0],pre[1]=mx[1],pre[2]=mx[2],pre[3]=mx[3];
                mx[0]=mx[1]=mx[2]=mx[3]=0;
            }
            x=pnt[x].x,y=pnt[p[i]].y;
            dp[i]=cmax(pre[0]-x-y,cmax(pre[1]+x-y,cmax(pre[2]-x+y,pre[3]+x+y)))+(ll)pnt[p[i]].b;
            mx[0]=cmax(mx[0],dp[i]+x+y);
            mx[1]=cmax(mx[1],dp[i]-x+y);
            mx[2]=cmax(mx[2],dp[i]+x-y);
            mx[3]=cmax(mx[3],dp[i]-x-y);
        }
        register ll ans=0;
        for (ri i(1);i<=cnt;p(i)) ans=cmax(ans,dp[i]);
        printf("%lld\n",ans);
        return 0;
    }
}
int main() {return nanfeng::main();}

不要忘记开 \(long\;\;long\)