Limitations of the Lipschitz constant as a defense against adversarial examples

目录

• 概
• 主要内容

Huster T., Chiang C. J. and Chadha R. Limitations of the lipschitz constant as a defense against adversarial examples. In European Conference on Machine Learning and Data Mining (ECML PKDD), 2018.

概

本文是想说明现有的依赖Lipschitz常数的以获得可验证的鲁棒性存在很大局限性.

主要内容

本文首先通过proposition 1 来说明在一定条件下, 存在一个鲁棒的模型:

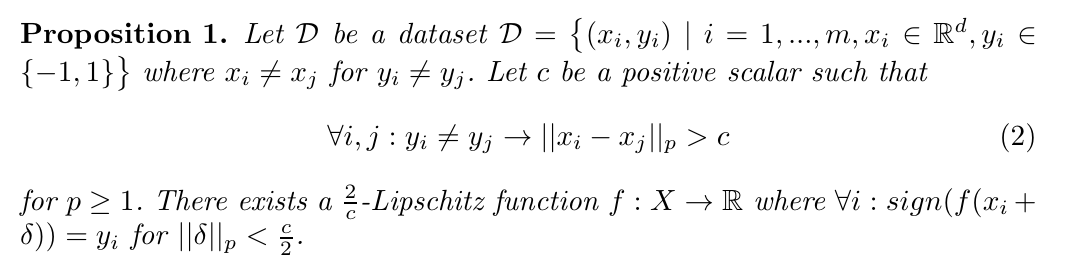
个人觉得这个证明或者这个条件有问题:

\[\forall i, j: y_i \not = y_j \rightarrow \|x_i - x_j\|_p > c,
\]

这个条件意味着:

\[\|x_i - x_j\|_p \le c \rightarrow y_i = y_j,
\]

但是这不就说明整个域都是一个类别? 所以初看这个条件时我以为就是对离散的部分点有效,

但是实际上我发现, 证明中这个条件时对于所有点适用的.

所以我不认可作者所说的低Lipschitz常数分类器有那么大的潜力.

我认为本文关于ReLU的论述, 即普通的ReLU的令变差变坏的结论是有意思的, 这个以后可能会用到(这不是恰恰说明了ReLU的局限性).