C. Hongcow Builds A Nation

C. Hongcow Builds A Nation

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Hongcow is ruler of the world. As ruler of the world, he wants to make it easier for people to travel by road within their own countries.

The world can be modeled as an undirected graph with n nodes and m edges. k of the nodes are home to the governments of the k countries that make up the world.

There is at most one edge connecting any two nodes and no edge connects a node to itself. Furthermore, for any two nodes corresponding to governments, there is no path between those two nodes. Any graph that satisfies all of these conditions is stable.

Hongcow wants to add as many edges as possible to the graph while keeping it stable. Determine the maximum number of edges Hongcow can add.

Input

The first line of input will contain three integers n, m and k (1 ≤ n ≤ 1 000, 0 ≤ m ≤ 100 000, 1 ≤ k ≤ n) — the number of vertices and edges in the graph, and the number of vertices that are homes of the government.

The next line of input will contain k integers c₁, c₂, ..., c_k (1 ≤ c_i ≤ n). These integers will be pairwise distinct and denote the nodes that are home to the governments in this world.

The following m lines of input will contain two integers u_i and v_i (1 ≤ u_i, v_i ≤ n). This denotes an undirected edge between nodes u_i and v_i.

It is guaranteed that the graph described by the input is stable.

Output

Output a single integer, the maximum number of edges Hongcow can add to the graph while keeping it stable.

Examples

Input

4 1 2
1 3
1 2

Output

2

Input

3 3 1
2
1 2
1 3
2 3

Output

0

Note

For the first sample test, the graph looks like this:

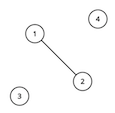Vertices 1 and 3 are special. The optimal solution is to connect vertex 4 to vertices 1 and 2. This adds a total of 2 edges. We cannot add any more edges, since vertices 1 and 3 cannot have any path between them.

For the second sample test, the graph looks like this:

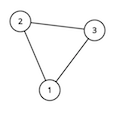We cannot add any more edges to this graph. Note that we are not allowed to add self-loops, and the graph must be simple.

题意：给你n个点，然后m条边，和k个特殊的点，问最多再能连多少条边，要求k个点是两两不联通的;

思路：并查集：

找出联通块，然后将没有那些特殊点的先合并再一块-->t，sum为答案，sum+=cnt[t]*(cnt[t]-1)/2-原来有的边，然后再在特殊的点中找含点最多的和他和并统计答案，并且加上其他特殊联通块最多能加的边。

  1 #include<iostream>
  2 #include<string.h>
  3 #include<algorithm>
  4 #include<queue>
  5 #include<math.h>
  6 #include<stdlib.h>
  7 #include<stack>
  8 #include<stdio.h>
  9 #include<ctype.h>
 10 #include<map>
 11 #include<vector>
 12 using namespace std;
 13 typedef long long LL;
 14 int c[100005];
 15 int bin[100005];
 16 int du[100005];
 17 vector<int>vec[100005];
 18 int fin(int x);
 19 int ask[100005];
 20 int id[100005];
 21 map<int,int>my;
 22 LL bian[100005];
 23 int main(void)
 24 {
 25     int n,m,k;
 26     int i,j;
 27
 28     while(scanf("%d %d %d",&n,&m,&k)!=EOF)
 29     {
 30         my.clear();
 31         memset(bian,0,sizeof(bian));
 32         for(i = 0; i <100005; i++)vec[i].clear(),bin[i] = i,du[i] = 1;
 33         for(i = 1; i <=k; i++)
 34             scanf("%d",&c[i]);
 35         while(m--)
 36         {
 37             int x,y;
 38             scanf("%d %d",&x,&y);
 39             vec[x].push_back(y);
 40             vec[y].push_back(x);
 41             int xx = fin(x);
 42             int yy = fin(y);
 43             if(xx!=yy)
 44             {
 45                 if(du[xx] > du[yy])
 46                 {
 47                     du[xx] += du[yy],bin[yy] = xx;
 48                     bian[xx]+=bian[yy];
 49                     bian[xx]++;
 50                 }
 51                 else
 52                 {
 53                     du[yy] += du[xx],bin[xx] = yy;
 54                     bian[yy]+=bian[xx];
 55                     bian[yy]++;
 56                 }
 57             }
 58             else bian[xx]++;
 59         }
 60         for(i = 1; i <= n; i++)
 61         {
 62             ask[i] = fin(i);
 63         }
 64         LL maxx = 0;
 65         LL b;
 66         for(i = 1; i <= k; i++)
 67         {
 68             my[ask[c[i]]] = 1;
 69             if(du[ask[c[i]]]>maxx)
 70             {
 71                 maxx = max((LL)du[ask[c[i]]],maxx);
 72                 b = bian[ask[c[i]]];
 73             }
 74         }
 75         LL cnt = 0;
 76         LL mc = 0;
 77         for(i = 1; i <= n; i++)
 78         {
 79             if(!my.count(ask[i]))
 80             {
 81                 cnt+=du[ask[i]];
 82                 my[ask[i]] = 1;
 83                 mc+=bian[ask[i]];
 84             }
 85         }//printf("%lld\n",maxx);
 86         LL acc = cnt*(cnt-1)/(LL)2;
 87         LL akk = acc;
 88         acc+=maxx*cnt;
 89         acc-=mc;
 90         for(i = 1;i <= k;i++)
 91         {
 92            acc+=(LL)du[ask[c[i]]]*(LL)(du[ask[c[i]]]-1)/(LL)2;
 93            acc-=bian[ask[c[i]]];
 94         }
 95         printf("%lld\n",acc);
 96     }
 97     return 0;
 98 }
 99 int fin(int x)
100 {
101     int i;
102     for(i = x; i!=bin[i];)
103         i = bin[i];
104     return i;
105 }