CF 476 div2 C

http://www.codeforces.com/contest/476/problem/C

 

C. Dreamoon and Sums

time limit per test

1.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Dreamoon loves summing up something for no reason. One day he obtains two integers a and b occasionally. He wants to calculate the sum of all nice integers. Positive integer x is called nice if 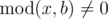 and 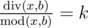, where k is some integer number in range[1, a].

By 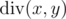 we denote the quotient of integer division of x and y. By  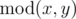we denote the remainder of integer division of x andy. You can read more about these operations here: http://goo.gl/AcsXhT.

The answer may be large, so please print its remainder modulo 1 000 000 007 (109 + 7). Can you compute it faster than Dreamoon?

Input

The single line of the input contains two integers a, b (1 ≤ a, b ≤ 107).

Output

Print a single integer representing the answer modulo 1 000 000 007 (109 + 7).

Examples

input

1 1

output

0

input

2 2

output

8

Note

For the first sample, there are no nice integers because 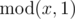 is always zero.

For the second sample, the set of nice integers is {3, 5}.

题目大意：给你一个公式，输入a和b，对于某满足(x / b) / (x % b) = k(1 <= k <= a)，问满足条件的x的总合

思路：我们得到x/b = k * （x%b），令x%b=i，然后枚举i即可得到相应的x = i * k * b + i，

然后即可得到暴力枚举的公式ans = ((1LL * i * ta % mod * b % mod + a * i % mod) % mod + ans) % mod，因此这种方法是O(b)的复杂度（ 无语了，这里因为中间的mod爆了LL导致后来卡了一会儿，果然做事需要谨慎点。）

当然如果把i提取出来还可以用O（1）的方法计算。

 //看看会不会爆int!数组会不会少了一维！
 //取物问题一定要小心先手胜利的条件
 #include <bits/stdc++.h>
 using namespace std;
 #define LL long long
 #define ALL(a) a.begin(), a.end()
 #define pb push_back
 #define mk make_pair
 #define fi first
 #define se second
 const int maxn =  + ;
 const LL mod = 1e9 + ;
 LL a, b;

 int main(){
     cin >> a >> b;
     LL ans = ;
     LL ta = (a + ) * a /  % mod;
     for (int i = ; i < b; i++){
         ans = ((1LL * i * ta % mod * b % mod + a * i % mod) % mod + ans) % mod;
     }
     printf("%I64d\n", ans);
     return ;
 }