trie从入门到入殓

trie是什么？1. 字典树 2.集合

（其实两个都对啊喂）

一颗普通的trie树一般类似于这样(图片来源于http://dongxicheng.org/structure/trietree/）：

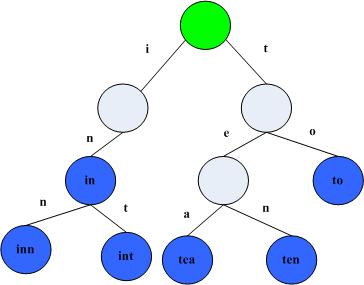
绿色的是根节点，如果字典集为全体小写字母的话，每一个节点就会有26个子节点（可以为空）。

（不过这些东西大佬们已经写了很多博客了在这里就不冗述了）

那么来看看trie的第二个十分十分十分重要的功能：集合。

如果不保存字母集，甚至不保存字符串，如果只保存“数”呢？

直接挂上maxlongint这么多的子节点？？？虽然只有一层（插入是O(1)），但是查询的话是O(n)的（因为无法有maxlongint的空间，所以查找相当于链表查找）。

或许会想到存储十进制下的每一位，不过怎么存呢？

从低位往高位存？好像只能检索某个数字是否存在，以及支持插入和删除，别忘了集合起码可以实现：插入、删除、查询某个数是否存在、查询某个数的排名、查询排名为k的数、查询某个数的前驱、查询某个数的后继。

（不过如果只需要判断某个数是否存在和插入以及删除的话，STL的map就已经实现了。）

先不说功能如何拓展，首先如果这么插入的话会发现树的高度与最大的那个数有关，看起来很不爽，那么就需要让它看起来比较好看，于是可以引入前导零了——把每个数都补成位数相同（在前面加上0）。

然后可以发现，这棵树最底层是插入的数的全集，但是遍历这颗树的时候从顶向下遍历比较舒服，于是就可以把这棵树重组一下了！从高位往低位进行插入！

这样的话会发现这棵树就可以支持所有的操作了！因为两个数字比较大小是可以从高位进行比较的！而且这些数的位数都相同所以从上往下遍历是可以实现的。

比如说查询排名，假设当前查到的数字的位数上的数为x，那么只要把同层所有小于x的数的size加一块就行了。

如果要查询第k大，那么就需要枚举一下当前位数以及之前位数的size之和，如果大于k的话就往当前位数左边走，否则往右面走，直到恰好小于k，然后k减掉这个值并递归到当前位数右面的那个位数后往下走。

（好像说的有点迷。。。不过这段其实没啥用。。。除非空间卡的很紧需要压一下位。。。不过那样的话还不如写个treap。。。）

然后可以发现这样的话代码实现太麻烦了，而且时间复杂度也变得很迷。

或许可以耗费一点空间而变得好写一些！比如说改成二进制！

改成二进制有如下几个好处：

1.计算机内存储的就是二进制，而且C/C++对位运算处理十分友善。

2.二进制下不是0就是1，不需要枚举所有的位数。

3.枚举位数十分好写，在本文后面的代码实现中可以看到。

对于排名查询和第k大查询跟前文的没什么区别，对于前驱和后继的话其实可以通过这两个而实现。

代码实现上，排名查询实际上返回的是小于该数的个数，而第k大查询正如其名。

那么来看一下前驱和后继如何查询（假设查询的这个数是x）：

1.前驱：x的前驱就是kth(rank(x))。小于x的个数事实上就是比x小且最大的那个数的排名。

2.后继：x的后继就是kth(rank(x+1)+1)。最后一个x的排名再往后一个排名就是第一个比x大的数的排名。

当然有利也有弊，01trie也带来了一些不好的地方：

1.空间消耗过大，如果有n个数字那么空间消耗为O(32n)，因为一个int是32字节。

2.不支持浮点数插入，当然有两种解决方式，第一种是离散化之后当成int来搞，不过一般题是不支持离线的样子，第二种是把浮点数拆成整数部分和小数部分，不过代价是空间复杂度的再一次上升。

在存储的时候有两种选择，一个是指针，一个是数组。

指针的话代码写起来比较符合人类的正常认知（从左到右），数组比较反人类（从里到外），不过有一种利用C/C++的地址运算符（方括号）实现的类指针写法（见本文后面的实现）。

但本文还并没有结束，01trie还有一种更有趣的用法，可以支持静态区间查询，也就是所谓的可持久化trie。

考虑新插入数的时候，建立一颗新的trie，然后每次查询[l,r]的时候将第r棵trie的出现次数与l-1棵trie的出现次数相减就是[l,r]的trie，然后就可以在这上面进行一系列trie的操作了。

但是，这么做的话空间复杂度是O(n^2)的，但是可以发现没有修改操作，每次只是添加一个数，也就是说只修改了一条链，那么每次只要将没修改的子节点接入到上一棵trie的子节点上就行。

附录一：tyvj平衡二叉树（01trie实现）

 #include <cstdio>
  * ;
 ], num[N], tot, root = ++ tot;
 #define walk for(int i = 31, rt = root, t ; ~i ; i --)
 #define cond(cd, st) if(x == cd) st;
 void ins(int val, int c) {
     val += (int)1e7;
     walk {
         ]) rt[ch][t] = ++ tot;
         (rt = rt[ch][t])[num] += c;
     }
 }
 , ) {
     val += (int)1e7;
     walk {
         )) ret += rt[ch][][num];
         rt = rt[ch][t];
     }
     return ret;
 }
 ) {
     walk
         ][num]) ret |=  << i, k -= rt[ch][][num], rt = rt[ch][];
         ];
     return ret - (int)1e7;
 }
 int main() {
     scanf("%d", &n);
     while(n --) {
         scanf("%d%d", &x, &y);
         cond(, ins(y, ));
         cond(, ins(y, -));
         cond(, printf());
         cond(, printf("%d\n", kth(y)));
         cond(, printf("%d\n", kth(rak(y))));
         cond(, printf() + )));
     }
 }