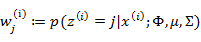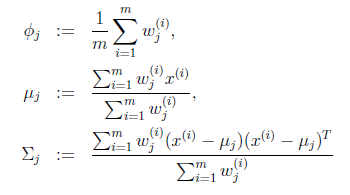混合高斯模型(Mixtures of Gaussians)和EM算法
这篇讨论使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation)。
与k-means一样,给定的训练样本是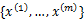 ,我们将隐含类别标签用
,我们将隐含类别标签用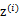 表示。与k-means的硬指定不同,我们首先认为
表示。与k-means的硬指定不同,我们首先认为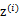 是满足一定的概率分布的,这里我们认为满足多项式分布,
是满足一定的概率分布的,这里我们认为满足多项式分布,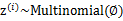 ,其中
,其中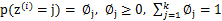 ,
,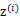 有k个值{1,…,k}可以选取。而且我们认为在给定
有k个值{1,…,k}可以选取。而且我们认为在给定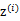 后,
后,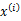 满足多值高斯分布,即
满足多值高斯分布,即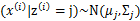 。由此可以得到联合分布
。由此可以得到联合分布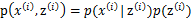 。
。
整个模型简单描述为对于每个样例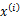 ,我们先从k个类别中按多项式分布抽取一个
,我们先从k个类别中按多项式分布抽取一个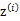 ,然后根据
,然后根据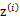 所对应的k个多值高斯分布中的一个生成样例
所对应的k个多值高斯分布中的一个生成样例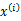 ,。整个过程称作混合高斯模型。注意的是这里的
,。整个过程称作混合高斯模型。注意的是这里的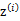 仍然是隐含随机变量。模型中还有三个变量
仍然是隐含随机变量。模型中还有三个变量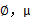 和
和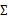 。最大似然估计为
。最大似然估计为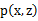 。对数化后如下:
。对数化后如下:
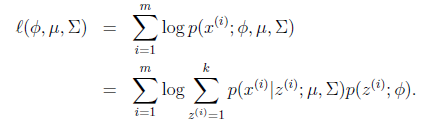
这个式子的最大值是不能通过前面使用的求导数为0的方法解决的,因为求的结果不是close form。但是假设我们知道了每个样例的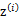 ,那么上式可以简化为:
,那么上式可以简化为:
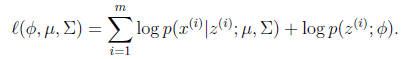
这时候我们再来对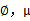 和
和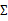 进行求导得到:
进行求导得到:
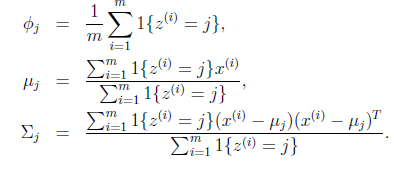
 就是样本类别中
就是样本类别中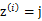 的比率。
的比率。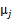 是类别为j的样本特征均值,
是类别为j的样本特征均值,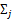 是类别为j的样例的特征的协方差矩阵。
是类别为j的样例的特征的协方差矩阵。
实际上,当知道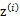 后,最大似然估计就近似于高斯判别分析模型(Gaussian discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
后,最大似然估计就近似于高斯判别分析模型(Gaussian discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
之前我们是假设给定了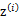 ,实际上
,实际上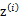 是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
|
循环下面步骤,直到收敛: { (E步)对于每一个i和j,计算
(M步),更新参数:
} |
在E步中,我们将其他参数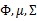 看作常量,计算
看作常量,计算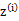 的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,
的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,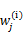 值又不对了,需要重新计算,周而复始,直至收敛。
值又不对了,需要重新计算,周而复始,直至收敛。
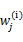 的具体计算公式如下:
的具体计算公式如下:
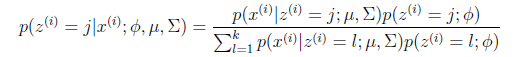
这个式子利用了贝叶斯公式。
这里我们使用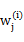 代替了前面的
代替了前面的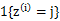 ,由简单的0/1值变成了概率值。
,由简单的0/1值变成了概率值。
对比K-means可以发现,这里使用了“软”指定,为每个样例分配的类别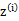 是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
混合高斯模型(Mixtures of Gaussians)和EM算法的更多相关文章
- 混合高斯模型的EM求解(Mixtures of Gaussians)及Python实现源代码
今天为大家带来混合高斯模型的EM推导求解过程. watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQveHVhbnl1YW5zZW4=/font/5a6L5L2T/ ...
- 混合高斯模型(Mixtures of Gaussians)
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html 这篇讨论使用期望最大化算法(Expectation-Maximizat ...
- <转>与EM相关的两个算法-K-mean算法以及混合高斯模型
转自http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html http://www.cnblogs.com/jerrylead/ ...
- EM相关两个算法 k-mean算法和混合高斯模型
转自http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html http://www.cnblogs.com/jerrylead/ ...
- PRML读书会第九章 Mixture Models and EM(Kmeans,混合高斯模型,Expectation Maximization)
主讲人 网络上的尼采 (新浪微博: @Nietzsche_复杂网络机器学习) 网络上的尼采(813394698) 9:10:56 今天的主要内容有k-means.混合高斯模型. EM算法.对于k-me ...
- 记录:EM 算法估计混合高斯模型参数
当概率模型依赖于无法观测的隐性变量时,使用普通的极大似然估计法无法估计出概率模型中参数.此时需要利用优化的极大似然估计:EM算法. 在这里我只是想要使用这个EM算法估计混合高斯模型中的参数.由于直观原 ...
- EM算法与混合高斯模型
非常早就想看看EM算法,这个算法在HMM(隐马尔科夫模型)得到非常好的应用.这个算法公式太多就手写了这部分主体部分. 好的參考博客:最大似然预计到EM,讲了详细样例通熟易懂. JerryLead博客非 ...
- 混合高斯模型(GMM)推导及实现
作者:桂. 时间:2017-03-20 06:20:54 链接:http://www.cnblogs.com/xingshansi/p/6584555.html 声明:欢迎被转载,不过记得注明出处哦 ...
- [zz] 混合高斯模型 Gaussian Mixture Model
聚类(1)——混合高斯模型 Gaussian Mixture Model http://blog.csdn.net/jwh_bupt/article/details/7663885 聚类系列: 聚类( ...
随机推荐
- selenium、python、firefox版本配合无敌
selenium (2.53.6) .python2.7.13. firefox46.0.1 完美
- 使用TCP/IP Monitor监视Soap协议
什么是soap? soap,简单对象访问协议,基于http传输xml数据,soap协议体是xml格式. SOAP 是一种网络通信协议 SOAP即Simple Object Access Protoco ...
- bootstrap 基础(二)
1 栅格系统偏移 栅格系统的偏移只能向右:col-xs-offset-x. <!DOCTYPE html> <html lang="en"> <hea ...
- 【小白成长撸】--顺序栈(C语言版)
// 顺序栈.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h"//test1.0--栈表仅限Int类型 #include <stdio. ...
- 为什么可以通过URL来调起APP - URL Scheme和Intent
在手机浏览器中可以通过URL调起APP是不是很神奇?这篇文章就告诉你为什么. URL Scheme 先从前端能接触到的URL Scheme分析一下 丢wiki:https://en.wikipedia ...
- Jquery 绑定标签事件
为子元素绑定: $('#foreachResult').delegate('td', 'click', function () { alert($(this).text()); ...
- NFA的实现
此次发表的是一个不确定的自动机(NFA),它可以根据输入的正规式输出由函数映像表示的结果. 此版本可以输入括号'(',')',但是,实现的过程理解起来有点吃力,所以,在时间允许的情况下,我还将写新文章 ...
- java课程设计——博客作业教学数据分析系统(201521123083 戴志斌)
目录 一.团队课程设计博客链接 二.个人负责模块或任务说明 三.自己的代码提交记录截图 四.自己负责模块或任务详细说明 五.课程设计感想 (题外话,终于可以用markdown建目录) 一.团队课程设计 ...
- 软件工程HW1-四则运算软件
题目描述 程序自动生成小学四则运算题目,用户输入每道题的答案之后,将答错的题目标出并计算此次答题的正确率. 项目链接 我的项目 项目运行截图 个人软件过程 此次开发的四个步骤: 1):需求分析 2): ...
- 团队作业——Alpha冲刺之事后诸葛亮
小组成员: 武健男:201421123091 林俊鹏:201421123076 何跃斌:201421123082 陈鑫龙:201421123078 潘益靖:201421123086 黄睿:201421 ...