2018ACM-ICPC亚洲区域赛南京站I题Magic Potion(网络流)

http://codeforces.com/gym/101981/attachments

题意：有n个英雄，m个敌人，k瓶药剂，给出每个英雄可以消灭的敌人的编号。每个英雄只能消灭一个敌人，但每个英雄只能消灭一个敌人。现在有药剂，英雄喝了之后可以多消灭一个敌人，但每个英雄只能喝一瓶，问最多能消灭多少个敌人。

下午在实验室队内自己开训练，和JC大佬那队一起开的，当时JC大佬他们队开的J题，没有看I题，当我们队AC之后JC大佬才看了I题，听到他们说，这题就差直接把网络流三个字写在题目里了。确实非常明显，很明显的一个匹配问题，如果每个英雄只能消灭一个敌人的话就是二分图匹配网络流裸题。刚开始建图错误，建成了这样。

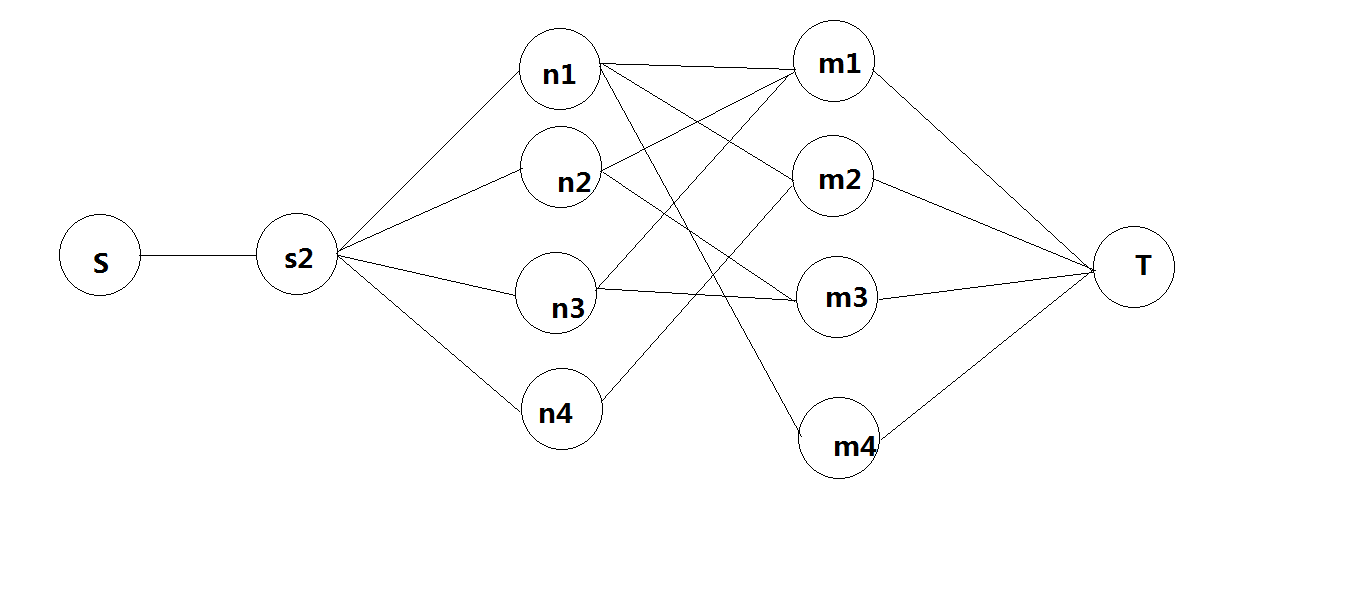
直接把s和s2直接连了一条n+k的边，s2和n个英雄直接建了一条边权为2的边，然后WA了一发。后面发现，有部分英雄如果没有消灭敌人，可能会被当成药剂给别的英雄。

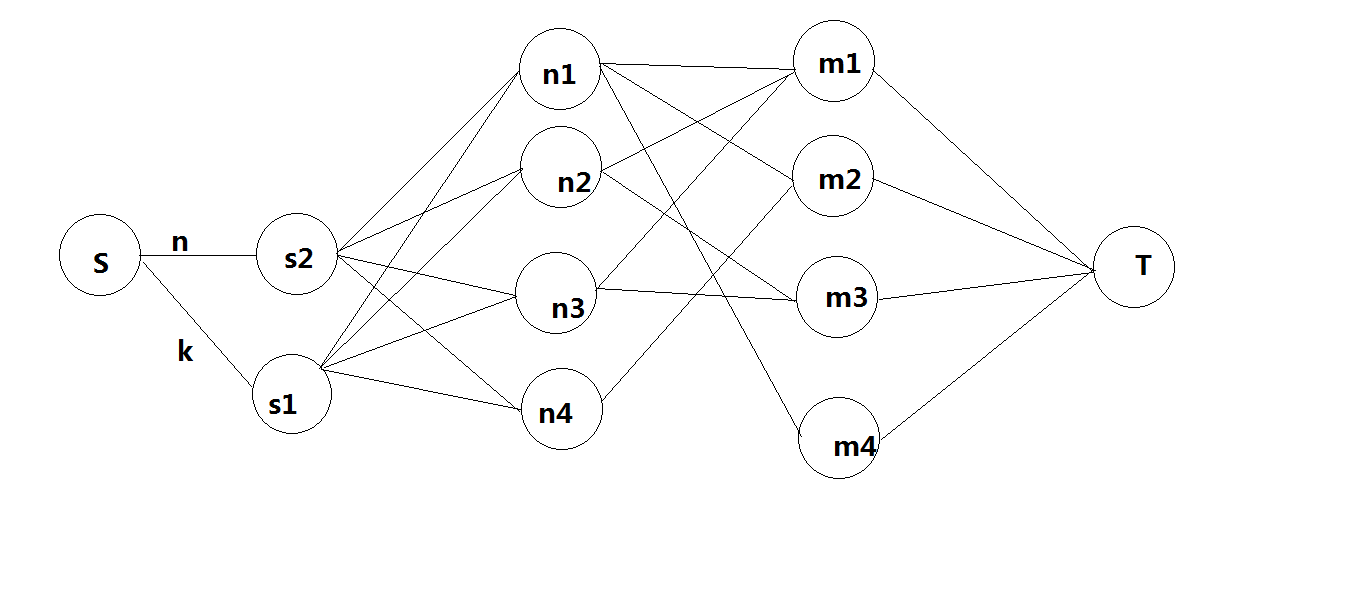
然后找到了正确建图方式，就是这样将药剂和每个英雄的攻击一次分离。在这张图上直接跑最大流就可以了。

最后贴上AC代码

#include<bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <int,int> pii;
#define rep(i,x,y) for(int i=x;i<y;i++)
#define rept(i,x,y) for(int i=x;i<=y;i++)
#define per(i,x,y) for(int i=x;i>=y;i--)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define de(x) cout<< #x<<" = "<<x<<endl
#define dd(x) cout<< #x<<" = "<<x<<" "
#define mes(a,b) memset(a,b,sizeof a)
const ll inf= 1e18;
const int N=2005,M=1e6;
int head[N],ver[M],edge[M],Next[M],d[N];
int n,m,s,t,tot,maxflow;
queue<int>q;

void add(int x,int y,int z)
{
    ver[++tot]=y,edge[tot]=z,Next[tot]=head[x],head[x]=tot;
    ver[++tot]=x,edge[tot]=0,Next[tot]=head[y],head[y]=tot;
}
bool bfs()
{
    mes(d,0);
    while(!q.empty()) q.pop();
    q.push(s);
    d[s]=1;
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        for(int i=head[x];i;i=Next[i])
        {
            if(edge[i]&&!d[ver[i]])
            {
                q.push(ver[i]);
                d[ver[i]]=d[x]+1;
                if(ver[i]==t) return 1;
            }
        }
    }
    return 0;
}
int dinic(int x,ll flow)
{
    if(x==t) return flow;
    int rest=flow,k;
    for(int i=head[x];i&&rest;i=Next[i])
    {
        if(edge[i]&&d[ver[i]]==d[x]+1)
        {
            k=dinic(ver[i],min(rest,edge[i]));
            if(!k) d[ver[i]]=0;
            edge[i]-=k;
            edge[i^1]+=k;
            rest-=k;
        }
    }
    return flow-rest;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    tot=1;
    int n,m,k;
    cin>>n>>m>>k;
    s=0;
    t=n+m+1;
    int s1=n+m+2,s2=n+m+3;
    rept(i,1,n)
    {
        int cnt;
        cin>>cnt;
        rept(j,1,cnt)
        {
            int y;
            cin>>y;
            add(i,n+y,1);
        }
    }
    add(s,s1,n);
    add(s,s2,k);
    rept(i,1,n) add(s1,i,1),add(s2,i,1);
    rept(i,1,m) add(n+i,t,1);
    int flow=0;
    while(bfs())
        while(flow=dinic(s,inf)) maxflow+=flow;
    cout<<maxflow<<"\n";
    return 0;
}