AOV网络拓扑排序
这个算法,主要是为输出一个无环图的拓扑序列
算法思想:
主要依赖一个栈,用来存放没有入度的节点,每次读取栈顶元素,并将栈顶元素的后继节点入度减一,如果再次出现入度为零的节点,就加入到栈中。参考《大话数据结构》,写下下面完整代码,并发现,其中程序的进行,出现错误。v6执行完,应该执行v9,因为此时v9是站顶元素,并不是v0.
算法流程:
int topGraph(graph g){
EdgeNode *e;
int i,k,gettop;
int top = ;
int count = ;
int *stack;
stack = (int *)malloc(g->numVertexes * sizeof(int));
for(i=;i<g->numVertexes;i++){
if(g->headlist[i].in == ) //把入度为0的,即没有入度的点入栈
stack[++top] = i;
}
while(top){
gettop = stack[top--];
printf("%d ",gettop);
count++;
for(e = g->headlist[gettop].fnode; e ; e=e->next){ //一次遍历链表,减少各个子节点的入度
k = e->data;
if(!(--g->headlist[k].in))
stack[++top] = k;
}
}
if(count < g->numVertexes)
return ERROR;
else
return OK;
}
全部代码:
#include <stdio.h>
#include <stdlib.h>
#define MAX 14
#define ERROR 1
#define OK 0
typedef struct edgeNode{
int data;
struct edgeNode *next;
}EdgeNode;
typedef struct headNode{
int in;
int data;
EdgeNode *fnode;
}HeadNode,HeadList[MAX];
typedef struct{
HeadList headlist;
int numEdges,numVertexes;
}Graph,*graph; void initGraph(graph g);
int inputInfo(graph g,int tar,int in,int data,int first);
void printGraph(graph g);
int topGraph(graph g);
int main(){
Graph *g = (Graph *)malloc(sizeof(Graph));
initGraph(g);
printGraph(g); if(topGraph(g) == ERROR)
printf("有环路!\n");
else
printf("没有环路!\n"); free(g);
getchar();
return ;
}
int topGraph(graph g){
EdgeNode *e;
int i,k,gettop;
int top = ;
int count = ;
int *stack;
stack = (int *)malloc(g->numVertexes * sizeof(int));
for(i=;i<g->numVertexes;i++){
if(g->headlist[i].in == ) //把入度为0的,即没有入度的点入栈
stack[++top] = i;
}
while(top){
gettop = stack[top--];
printf("%d ",gettop);
count++;
for(e = g->headlist[gettop].fnode; e ; e=e->next){ //一次遍历链表,减少各个子节点的入度
k = e->data;
if(!(--g->headlist[k].in))
stack[++top] = k;
}
}
if(count < g->numVertexes)
return ERROR;
else
return OK;
}
void printGraph(graph g){
int i;
printf("vertex:%d,edges:%d\n",g->numVertexes,g->numEdges);
EdgeNode *e = (EdgeNode *)malloc(sizeof(EdgeNode));
for(i=;i<MAX;i++){
printf("[in:%d]%d",g->headlist[i].in,g->headlist[i].data);
e = g->headlist[i].fnode;
while(e != NULL){
printf("->%d",e->data);
e = e->next;
}
printf("\n");
}
free(e);
}
void initGraph(graph g){
g->numVertexes = MAX;
g->numEdges = ;
int i;
for(i=;i<MAX;i++){
g->headlist[i].fnode = NULL;
}
inputInfo(g,,,,);
inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,); inputInfo(g,,,,-); inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,); inputInfo(g,,,,-); inputInfo(g,,,,); inputInfo(g,,,,-);
}
int inputInfo(graph g,int tar,int in,int data,int first){
g->numEdges++; if(first == -){ //没有后继的边节点
g->headlist[tar].in = in;
g->headlist[tar].data = data;
return ;
} if(!g->headlist[tar].fnode){ //观察是否已经初始化
g->headlist[tar].in = in;
g->headlist[tar].data = data;
}
EdgeNode *e = (EdgeNode *)malloc(sizeof(EdgeNode));
e->data = first;
e->next = g->headlist[tar].fnode;
g->headlist[tar].fnode = e;
return ;
}
执行示例:
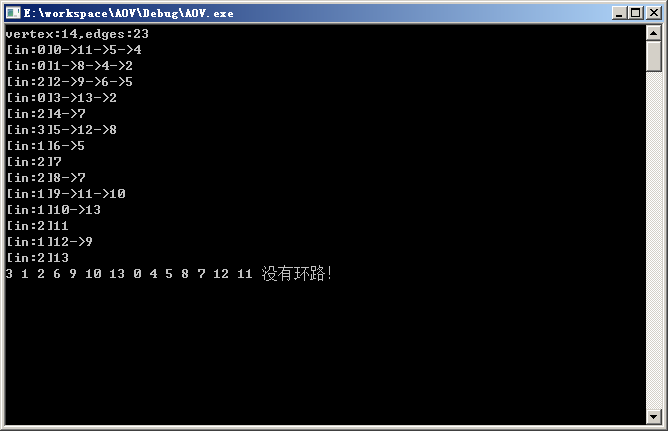
AOV网络拓扑排序的更多相关文章
- AOV拓扑排序实验总结-1
AOV拓扑排序实验总结-1 实验数据:1.实验输入数据在input.txt文件中2.对于n是指有顶点n个,数据的结束标志是一行0 0. 实验目的:获取优秀的AOV排序算法模板 数据结构安排 ...
- AOV拓扑排序实验-2-AOV类的实现
下面是这个类的实现代码: //这只是一个基本的框架,没有封装 #include<iostream> #include<cstdio> #include<malloc.h& ...
- 设计AOV网拓扑排序的算法
拓扑排序 对一个有向图构造拓扑序列的过程称为拓扑排序(不唯一) 思想 从AOV网选择一个没有前驱的顶点并输出 从AOV网中删去该顶点,并且删去所有以该顶点为尾的弧 重复上述两步,直到全部顶点都被输出, ...
- [SOJ] Ordering Tasks
1940. Ordering Tasks Constraints Time Limit: 1 secs, Memory Limit: 32 MB Description John has n task ...
- Hadoop 基石HDFS 一文了解文件存储系统
@ 目录 前言:浅谈Hadoop Hadoop的发展历程 1.1 Hadoop产生背景 1.引入HDFS设计 1.1 HDFS主要特性 2.HDFS体系结构 HDFS工作流程机制 1.各个节点是如何互 ...
- 算法与数据结构(七) AOV网的拓扑排序
今天博客的内容依然与图有关,今天博客的主题是关于拓扑排序的.拓扑排序是基于AOV网的,关于AOV网的概念,我想引用下方这句话来介绍: AOV网:在现代化管理中,人们常用有向图来描述和分析一项工程的计划 ...
- 有向无环图的应用—AOV网 和 拓扑排序
有向无环图:无环的有向图,简称 DAG (Directed Acycline Graph) 图. 一个有向图的生成树是一个有向树,一个非连通有向图的若干强连通分量生成若干有向树,这些有向数形成生成森林 ...
- AOV网络和Kahn算法拓扑排序
1.AOV与DAG 活动网络可以用来描述生产计划.施工过程.生产流程.程序流程等工程中各子工程的安排问题. 一般一个工程可以分成若干个子工程,这些子工程称为活动(Activity).完成了这些活动 ...
- 算法与数据结构(七) AOV网的拓扑排序(Swift版)
今天博客的内容依然与图有关,今天博客的主题是关于拓扑排序的.拓扑排序是基于AOV网的,关于AOV网的概念,我想引用下方这句话来介绍: AOV网:在现代化管理中,人们常用有向图来描述和分析一项工程的计划 ...
随机推荐
- UVa 10969 (圆与圆之间的覆盖问题) Sweet Dream
题意: 有n个按先后顺序放置的不同大小不同位置的圆,求所有可见圆弧的长度. 分析: 这道题应该是大白书上例题 LA 2572 (求可见圆盘的数量) Kanazawa 的加强版,整体框架都差不多. 对于 ...
- 如何让Vim显示dos下的^M符号
/*********************************************************************** * 如何让Vim显示dos下的^M符号 * 声明: * ...
- webapp调试工具weinre的使用
在设计师与前端开发人员的努力下,一个WebApp出炉了,可是测试人员说了一堆的问题:某某机型下页面表现不一致,某某系统下页面如何如何,某某 系统浏览器下页面怎么怎么滴.看着满满的测试汇总文档,我们曾经 ...
- 流媒体相关知识介绍 及其 RTP 应用
一.流媒体简介 随着Internet的日益普及,在网络上传输的数据已经不再局限于文字和图形,而是逐渐向声音和视频等多媒体格式过渡.目前在网络上传输音频/视频(Audio/Video,简称A/V)等多媒 ...
- Delphi EVariantTypeCastError错误的解决方法
在执行程序的时候总是提示: ---------------------------Debugger Exception Notification---------------------------P ...
- Windows环境自动获取AWR报告
1.双击awr.cmd,通过cmd窗口运行awr.sql cmd.exe /c sqlplus lcam_1230/zcpzg1z_1230@54_orcl @awr.sql awr.cmd 2.aw ...
- 9月5日 华为2014校园招聘的机试题目_C语言版答案
手有些生了. 题目: 通过键盘输入一串小写字母(a~z)组成的字符串.请编写一个字符串压缩程序,将字符串中连续出席的重复字母进行压缩,并输出压缩后的字符串.压缩规则:1.仅压缩连续重复出现的字符.比如 ...
- ZOJ3865:Superbot(BFS) The 15th Zhejiang University Programming Contest
一个有几个小坑的bfs 题目很长,但并不复杂,大概总结起来有这么点. 有t组输入 每组输入n, m, p.表示一个n*m的地图,每p秒按键会右移一次(这个等会儿再讲). 然后是地图的输入.其中'@'为 ...
- .net-C#代码判断
ylbtech-doc:.net-C#代码判断 C#代码判断 1.A,C#代码判断返回顶部 01.{ C#题目}public static void Main(string[] args){ ...
- String.valueOf()
1. 由 基本数据型态转换成 String String 类别中已经提供了将基本数据型态转换成 String 的 static 方法 也就是 String.valueOf() 这个参数多载的方法 有下 ...
