【高斯消元】Poj 1222:EXTENDED LIGHTS OUT

---

Description

　　In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right. 

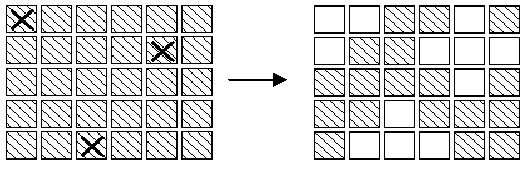
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged. 

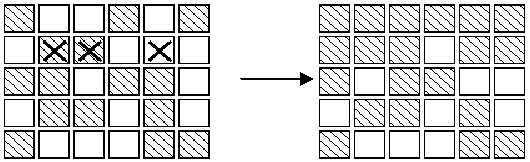
Note: 
1. It does not matter what order the buttons are pressed. 
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once. 
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first 
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off. 
Write a program to solve the puzzle.

Input

　　The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.

Output

　　For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.

---

　　翻译：给你一个5*6的初始状态，要求你给出一个5*6的操作矩阵，要求：当操作是1时，代表把棋盘的对应位置和它相邻的地方的状态改变（1变为0,0变为1），0则不进行操作。要求操作矩阵满足操作后棋盘状态全部为0.保证有解且唯一

　　提示:按两下和不按是一样的，所以只有按不按，没有按几下的区别。也没有先按后按的区别。

　　就是解异或方程。。

　　每个点按不按^周围的点按不按^最开始情况=0

　　转换一下。。

　　周围的点^每个点按不按=最开始情况

　　枚举每个点，之后就是喜闻乐见的高斯消元时间了。。(ps.如果消i元素，但是你的f[i][i]=0的话，需要找一行不等于0的行swap一下)

　　代码：

　　

 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>

 using namespace std;

 int f[][],ans[][],ga[][],cnt=;

 void print()
 {
     cnt++;
     printf("PUZZLE #%d\n",cnt);
     for(int i=;i<=;i++)
     {
         for(int j=;j<=;j++)
             printf("%d ",ans[i][j]);
         printf("\n");
     }
 }

 void Solve()
 {
     for(int i=;i>=;i--)
     {
         int x=i/+,y=i%;
         if(!y)    y+=,x--;
         ans[x][y]=ga[i][];
         for(int j=i+;j<=;j++)
             if(ga[i][j]){
                 int x1=j/+,y1=j%;
                 if(!y1) y1+=,x1--;
                 ans[x][y]=ans[x][y]^ans[x1][y1];
             }
     }
 }

 void swapp(int l,int r)
 {
     for(int i=;i<=;i++)
         swap(ga[l][i],ga[r][i]);
 }

 void find(int n)
 {
     for(int i=n+;i<=;i++)
         if(ga[i][n]){swapp(i,n);return;}
 }

 void Guass()
 {
     for(int i=;i<=;i++)//消第几个元
     {
         if(!ga[i-][i-])find(i-);
         if(!ga[i-][i-])continue;
         for(int j=i;j<=;j++)//第几个方程
         {
             if(!ga[j][i-])continue;
             for(int k=i;k<=;k++)//方程的第几项
                 ga[j][k]=ga[j][k]^ga[i-][k];
         }
     }
     Solve();
 }

 void set()
 {
     for(int i=;i<=;i++)
         for(int j=;j<=;j++){
             ga[(i-)*+j][]=f[i][j];
             ga[(i-)*+j][(i-)*+j]=;                //自己和上下左右是对自己有影响的点
             if(j!=) ga[(i-)*+j][(i-)*+j-]=;
             if(j!=) ga[(i-)*+j][(i-)*+j+]=;
             if(i!=) ga[(i-)*+j][i*+j]=;
             if(i!=) ga[(i-)*+j][(i-)*+j]=;
         }
     return;
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         for(int i=;i<=;i++)
             for(int j=;j<=;j++)
                 scanf("%d",&f[i][j]);
         set();
         Guass();
         print();
         memset(f,,sizeof(f));
         memset(ga,,sizeof(ga));
         memset(ans,,sizeof(ans));
     }
     return ;
 }