TCP 粘包及其解决方案(zz)

首先，我们回顾一下 TCP 和 UDP 的头部信息：

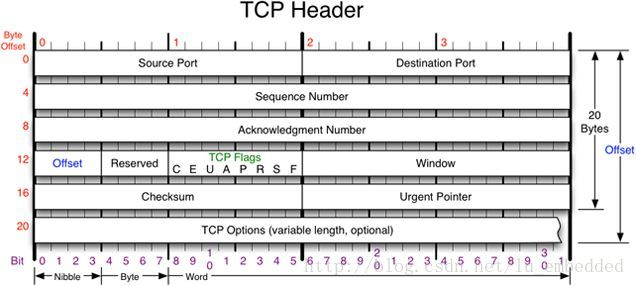
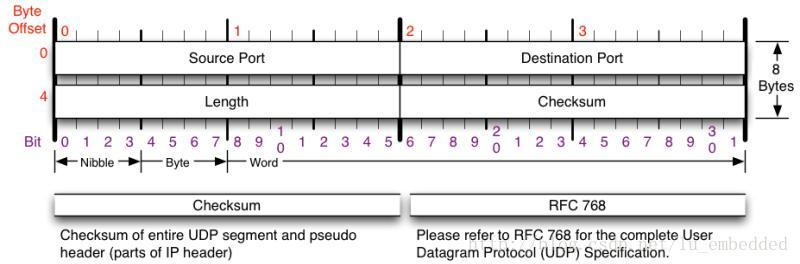
具体说明看：http://www.cnblogs.com/aomi/p/7776582.html

我们知道，TCP 和 UDP 是 TCP/IP 协议族传输层中的两个具有代表性的协议。其中，TCP 是面向连接的复杂的、可靠的字节流传输协议，而 UDP 是面向无连接的简单的、不可靠的数据报传输协议。 
　　“流”的概念就是指不间断的数据结构，可以把它想象成你们家里的自来水管道中的水流。什么意思呢？举个例子：TCP 发送端应用程序发送了10次100字节的消息，那么，在接收端的应用程序接收到的可能是一个1000字节的连续不间断的数据。但如果是 UDP 端口发送了一个100字节的消息，那么 UDP 接收端就会以100字节的长度来接收数据。正因为这样，我们可以看到 TCP 头部中并没有长度信息，而 UDP 头部包含长度信息。好了，现在你应该明白我们在创建套接字的时候，为什么 type 的类型是 SOCK_STREAM 和 SOCK_DGRAM 了吧！ 
　　

正如文章标题所述，显然，你已经知道 UDP 数据包存在明确边界，是不存在粘包现象的，只有 TCP 才会出现粘包现象。那么，接下来我们逐步分析 TCP 的流传输特性所带来如粘包这样的一些问题及其解决方案。

　　按每次通信后是否闭关连接，可以分为两类情况：长连接和短连接。长连接——指的是客户端和服务端先建立通信连接，连接建立后不断开，然后再进行报文发送和接收。短连接——指的是客户端和服务端每进行一次报文收发交易时才进行通信连接，交易完毕后立即断开连接，比如 http 协议。 
　　所以我们可以分析以下几种情况： 
　　（1）如果利用 TCP 每次发送数据，就与对方建立连接，然后双方发送完一段数据后，就关闭连接，这样就不会出现粘包问题（因为只有一种数据结构）。 
　　（2）如果发送数据无结构，如文件传输，这样发送端只管发送，接收端只管接收存储就行，也不用考虑粘包。 
　　（3）如果双方建立连接，需要在连接后一段时间内发送多个不同结构的数据，这时候接收端收到就可能是一堆粘在一起的数据，这样接收端应用程序就傻了，到底是要干嘛？不知道，因为协议并没有规定这么诡异的数据。 
　　 
　　那么，可以认为 TCP 粘包问题并不是对所有应用都造成困扰的，只是对那些长连接并且需要传输多种数据结构的应用造成影响。仔细分析会发现，除了粘包问题，其实还可能会出现多包、少包、半包、断包等情况。

针对这些问题，一般会有如下解决方法： 
　　（1）调用发送函数之后都强制数据立即传送（PUSH 指令）。 
　　（2）对于接收端引起的粘包，则可通过优化程序设计、精简接收进程工作量、提高接收进程优先级等措施，使其及时接收数据，从而尽量避免出现粘包现象。 
　　（3）添加一个固定的消息头，该消息头包含数据长度信息，每次数据时先接收固定大小的消息头，再根据其携带的长度信息接收消息实体。也就是说，通过人为控制多次接收来避免粘包。 
　　（4）设置 TCP_NODELAY 选项，禁止 Nagle 算法。 
　　（5）设置 SO_RCVBUF 和 SO_SNDBUF 选项，根据应用需求修改一个合适的接收、发送缓冲区大小。 
　　（6）添加报文分隔标识，比如发送报文是在末尾添加 '\n' ，同时接收端使用 recv() 函数接收报文，并且设置参数 flags 的值为 MSG_PEEK。注意：当 flags 参数的值设置为 MSG_PEEK 时，recv() 可以从 socket 缓存中读取数据，但是不会将缓存中该部分数据清除，但如果使用 read() 函数直接读取 socket 缓存区中的内容，会清空缓存区中的内容。假设两段报文粘包，read() 会清空缓存区中所有内容，从而导致后一段报文中的粘包的部分数据丢失。

　　实际上，上述的几种解决方法都有不足之处，并且不一定能够完全避免 TCP 粘包问题。所以还是需要根据实际应用来进行应用场景和性能方面的衡量。

参考： 
【1】Socket粘包问题 
【2】Socket/TCP粘包、多包和少包, 断包 
【3】（经典）tcp粘包分析 
【4】Linux 网络编程详解五（TCP/IP协议粘包解决方案二）

 

顶

1

踩