可持久化线段树（主席树）快速简洁教程 图文并茂 保证学会。kth number例题

如果学不会也不要打我。

假设你会线段树

开始！

主席树也叫可持久化线段树

顾名思义，它能够保存线段树在每个时刻的版本。

什么叫每个时刻的版本？你可能对一棵普通线段树进行各种修改，这每种样子就是我们所说的不同时刻的版本。

假设我们对线段树进行单点修改，维护区间和。

每次修改操作中，只有logn个节点会被修改，我们可以复制这些被修改的节点，而不复制没有被改变的节点（以提高效率）。

最后通过特殊的方式建立出新时刻的树。

建造方式如下：

假设上一时刻的树长这样：

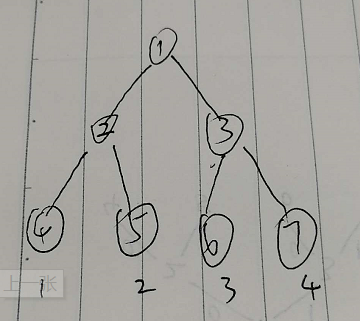
现在进行修改操作，对下标为3的位置修改，也就是说修改1 3 6号节点。若是普通线段树，则直接修改1 3 6三个节点。但是在主席树中，我们不直接在1 3 6号节点上修改。而是新建3个节点，分别对应1 3 6号节点，对新建节点进行本想在1 3 6号节点进行的操作（“本想”指普通线段树）。

如图：

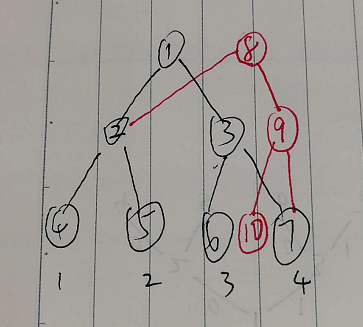
关于不同版本的线段树理解

接上图，可以观察到，1号和8号往下分别是两棵不同版本的线段树，不同版本共用很多节点。这并不会影响自上而下的查询。

单点修改的例子

以下内容质量不高：

寒羽吾:

用主席树做kth number，就是在空线段树的基础上，依次在线段树的位置a[1]处加一，a[2]处加一。即用线段树维护值在某区间中的ai有多少个。然后可以在线段树上移动指针，找到第k个。

寒羽吾:

考虑区间[l,r]的限制，即r时刻的线段树减去l-1时刻的线段树，就得到维护ai（下标i在[l,r]中）的线段树了。

寒羽吾:

查询的时候不必真把做差得到的线段树求出来，需要这个线段树的什么位置就访问r版本和l-1版本的对应点，取出值相减即可。

寒羽吾:

上面是我写的板子，t表示树节点，w[0]左孩子w[1]右孩子。

寒羽吾:

理论上维护21e9个元素的线段树是开不下节点的（也是时间上不可建立的），但因为主席树的特殊性：只建立需要用（改变）的节点。所以可以不对ai进行离散化，直接建立“看似”能维护21e9个元素的线段树。

#include<bits/stdc++.h>
using namespace std;
struct node{
	int sum;
	int w[2];
}t[5000005];
int np;
int n,m;
int st[100005];
int a[100005];
void plu(int x,int c,int num){
	int now=++np;
	t[now]=t[x];
	if(c<0){
		t[now].sum++;
		return;
	}
	int p=(num>>c)&1;
	plu(t[now].w[p],c-1,num);
	t[now].w[p]=now+1;
	t[now].sum=t[t[now].w[0]].sum+t[t[now].w[1]].sum;
}
int solve(int l,int r,int k){
	int lx=st[l-1],rx=st[r],ans=0;
	for(int i=0;i<=30;i++){
		int p=0;
		if(t[t[rx].w[0]].sum-t[t[lx].w[0]].sum<k)
			k-=t[t[rx].w[0]].sum-t[t[lx].w[0]].sum,
			p=1;
		lx=t[lx].w[p],
		rx=t[rx].w[p],
		ans=ans<<1|p;
	}
	return ans;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		a[i]+=1e9;
	}
	np=1;st[0]=1;
	for(int i=1;i<=n;i++){
		st[i]=np+1;
		plu(st[i-1],30,a[i]);
	}
	for(int i=1;i<=m;i++){
		int l,r,k;
		scanf("%d%d%d",&l,&r,&k);
		printf("%d\n",int(solve(l,r,k)-1e9));
	}
	return 0;
}