（数据科学学习手札14）Mean-Shift聚类法简单介绍及Python实现

不管之前介绍的K-means还是K-medoids聚类，都得事先确定聚类簇的个数，而且肘部法则也并不是万能的，总会遇到难以抉择的情况，而本篇将要介绍的Mean-Shift聚类法就可以自动确定k的个数，下面简要介绍一下其算法流程：

　　1.随机确定样本空间内一个半径确定的高维球及其球心；

　　2.求该高维球内质心，并将高维球的球心移动至该质心处；

　　3.重复2，直到高维球内的密度随着继续的球心滑动变化低于设定的阈值，算法结束

具体的原理可以参考下面的地址，笔者读完觉得说的比较明了易懂：

http://blog.csdn.net/google19890102/article/details/51030884

而在Python中，机器学习包sklearn中封装有该算法，下面用一个简单的示例来演示如何在Python中使用Mean-Shift聚类：

一、低维

from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from matplotlib.pyplot import style
import numpy as np
'''设置绘图风格'''
style.use('ggplot')
'''生成演示用样本数据'''
data1 = np.random.normal(0,0.3,(1000,2))
data2 = np.random.normal(1,0.2,(1000,2))
data3 = np.random.normal(2,0.3,(1000,2))

data = np.concatenate((data1,data2,data3))

# data_tsne = TSNE(learning_rate=100).fit_transform(data)
'''搭建Mean-Shift聚类器'''
clf=MeanShift()
'''对样本数据进行聚类'''
predicted=clf.fit_predict(data)
colors = [['red','green','blue','grey'][i] for i in predicted]
'''绘制聚类图'''
plt.scatter(data[:,0],data[:,1],c=colors,s=10)
plt.title('Mean Shift')

二、高维

from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from matplotlib.pyplot import style
import numpy as np
'''设置绘图风格'''
style.use('ggplot')
'''生成演示用样本数据'''
data1 = np.random.normal(0,0.3,(1000,6))
data2 = np.random.normal(1,0.2,(1000,6))
data3 = np.random.normal(2,0.3,(1000,6))

data = np.concatenate((data1,data2,data3))

data_tsne = TSNE(learning_rate=100).fit_transform(data)
'''搭建Mean-Shift聚类器'''
clf=MeanShift()
'''对样本数据进行聚类'''
predicted=clf.fit_predict(data)
colors = [['red','green','blue','grey'][i] for i in predicted]
'''绘制聚类图'''
plt.scatter(data_tsne[:,0],data_tsne[:,1],c=colors,s=10)
plt.title('Mean Shift')

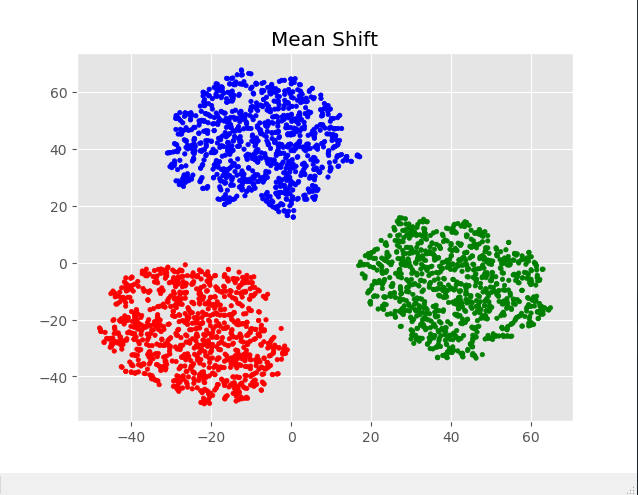
三、实际生活中的复杂数据

我们以之前一篇关于K-means聚类的实战中使用到的重庆美团商户数据为例，进行Mean-Shift聚类：

import matplotlib.pyplot as plt
from sklearn.cluster import MeanShift
from sklearn.manifold import TSNE
import pandas as pd
import numpy as np
from matplotlib.pyplot import style

style.use('ggplot')

data = pd.read_excel(r'C:\Users\windows\Desktop\重庆美团商家信息.xlsx')
input = pd.DataFrame({'score':data['商家评分'][data['数据所属期'] == data.iloc[0,0]],
                      'comment':data['商家评论数'][data['数据所属期'] == data.iloc[0,0]],
                      'sales':data['本月销售额'][data['数据所属期'] == data.iloc[0,0]]})

'''去缺省值'''
input = input.dropna()

input_tsne = TSNE(learning_rate=100).fit_transform(input)

'''创造色彩列表'''
with open(r'C:\Users\windows\Desktop\colors.txt','r') as cc:
    col = cc.readlines()
col = [col[i][:7] for i in range(len(col)) if col[i][0] == '#']

'''进行Mean-Shift聚类'''
clf = MeanShift()
cl = clf.fit_predict(input)

'''绘制聚类结果'''
np.random.shuffle(col)
plt.scatter(input_tsne[:,0],input_tsne[:,1],c=[col[i] for i in cl],s=8)
plt.title('Mean-Shift Cluster of {}'.format(str(len(set(cl)))))

可见在实际工作中的复杂数据用Mean-Shift来聚类因为无法控制k个值，可能会产生过多的类而导致聚类失去意义，但Mean-Shift在图像分割上用处很大。

以上便是本篇对Mean-Shift简单的介绍，如有错误望指出。