【题解】Journeys(线段树优化连边)

[#3073. Pa2011]Journeys （线段树优化连边）

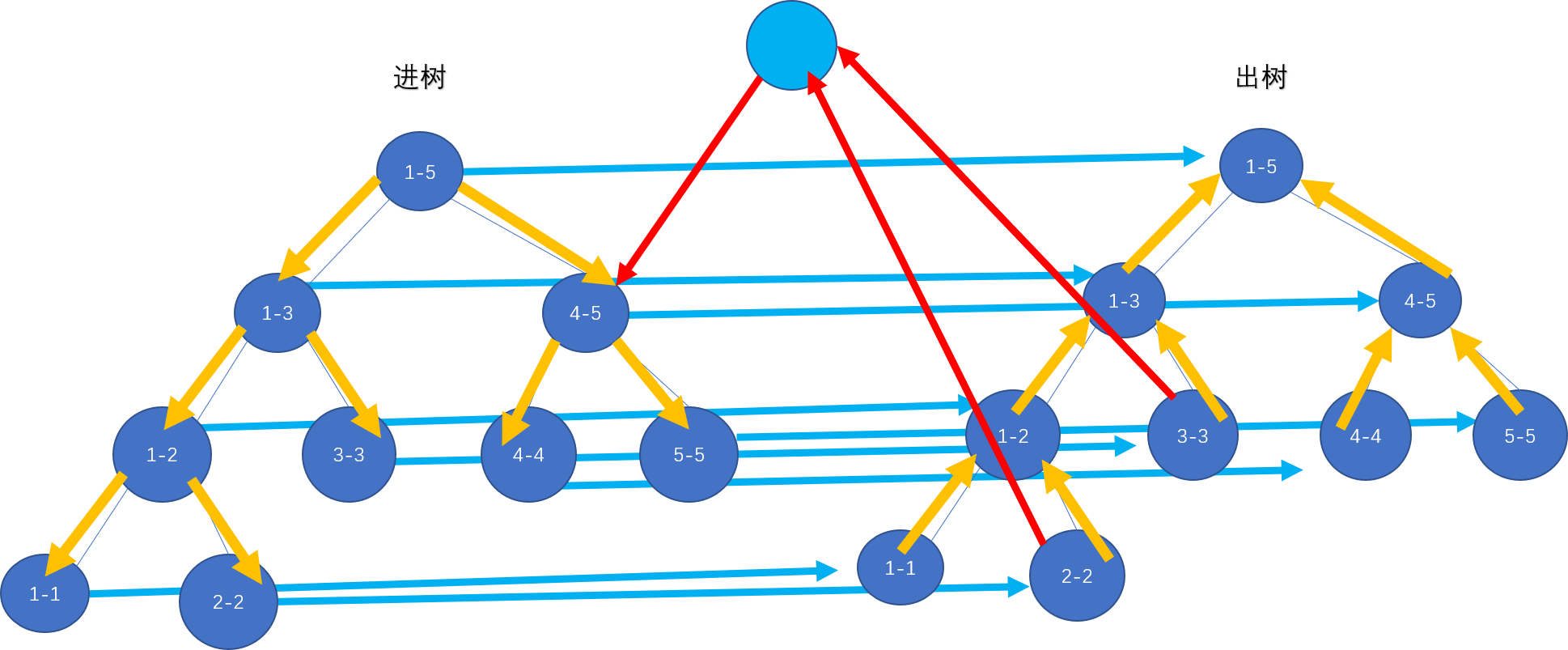
这张图太直观了，直接讲透了线段树优化连边的原理和正确性。

考虑建立两颗线段树，一颗是外向树，一颗是内向树，相当于网络流建模一样，我们可以利用这两颗线段树分别模拟一个点的入度和出度。毕竟一个点如果确定了它的入度和出度就相当于确定了在图中的位置。

外向树

一条边进入了一个父亲节点，相当于能进入它所有的儿子，这就模拟了入度。这和线段树很像，于是我们就做成线段树的样子，每次加边的时候，最多从外向树选出\(O(\log n)​\)的节点，就可以模拟出区间添加入度的操作。为了真正落实可以免费进入儿子的效果，我们每个节点向儿子连一条边权为0的边。

内向树

一条边从一个父亲节点出去，相当于他所有的儿子可以从这条边出去，这就模拟了出度。这和线段树很像，于是我们就做成线段树的样子，每次加边的时候，最多从外向树选出\(O(\log n)\)的节点，就可以模拟出区间添加出度的操作。为了真正落实可以免费从儿子出的效果，我们每个节点向父亲连一条边权为0的边。

两个操作加起来，就成功添加了一条有向边，边数是\(n\log n​\)级别的。

实现方式

每次要加边时，我们如果\(O(\log^2n)\)地加的话，就会导致边数多一个\(\log\)，所以我们新建一个点，再添加，就会用\(O(n)\)的点换来\(O(n \log n )\)的边数了。

线段树不一定真的要建出来(我觉得甚至用树状数组或者循环控制都行啊，因为我们主要是要得到一个二叉关系)。原图我们就可以丢了，原图的点就变成了外向树的叶子节点，对于这两颗线段树一起看做一个新图操作就好了。

由于从同一个点到同一个点是不用花费任何代价的，但是我们也不能有自环，所以我们从每个节点的入度节点到出度节点连一条边权为0的边。

代码人丑常数/内存都大，仅供参考。

//@winlere
#include<bits/stdc++.h>
using namespace std;  typedef long long ll;
template < class ccf > inline ccf qr(ccf ret){      ret=0;
      register char c=getchar();
      while(not isdigit(c)) c=getchar();
      while(isdigit(c)) ret=ret*10+c-48,c=getchar();
      return ret;
}inline int qr(){return qr(1);}
const int maxn=5e5;
int n,m,k,T;
int d[(int)(maxn*4.6)];
const int inf=1<<18;
typedef pair < int , int > P;

priority_queue < P , vector < P > , greater < P > > q;
struct E{unsigned long long to:30,w:2,nx:30;E(){to=w=nx=0;}E(const int&a,const int&b,const int&c){to=a;w=b;nx=c;}};
vector < E > e;
vector < int > v1,v2;
int head[(int)(maxn*4.6)];
int cnt;
inline void add(const int&fr,const int&to,const int&w){
      e.push_back(E(to,w,head[fr]));head[fr]=e.size()-1;
}

#define st first
#define nd second
#define midd register int mid=(l+r)>>1

#define lef l,mid,pos<<1
#define rgt mid+1,r,pos<<1|1
#define push(a,b) push(make_pair(a,b))
void build1(const int&l,const int&r,const int&pos){//外向树
      midd;T=max(pos,T);
      if(l==r)return;
      add(pos,pos<<1,0);add(pos,pos<<1|1,0);
      build1(lef);build1(rgt);
}

void build2(const int&l,const int&r,const int&pos){//内向树
      midd;
      if(l==r)return;
      add((pos<<1)+T,pos+T,0);add((pos<<1|1)+T,pos+T,0);
      build2(lef);build2(rgt);
}

void que(vector < int >&ve,const int&L,const int&R,const int&l,const int&r,const int&pos){
      if(L>r||R<l)return;midd;
      if(L<=l&&r<=R){ve.push_back(pos);return;}
      que(ve,L,R,lef);que(ve,L,R,rgt);
}

void ans(const int&l,const int&r,const int&pos){
      if(l==r){printf("%d\n",d[pos]);return;}
      midd;ans(lef);ans(rgt);
}

inline void dij(int S){
      for(register int t=1;t<=T;++t) d[t]=d[t+T]=inf,add(t,t+T,0);
      for(register int t=T<<1|1;t<=cnt;++t) d[t]=inf;
      d[S]=0;
      q.push(0,S);
      add(S+T,S,0);
      while(not q.empty()){
	    register P temp=q.top();q.pop();
	    for(register int t=head[temp.nd];t;t=e[t].nx)
		  if(d[e[t].to]>d[temp.nd]+e[t].w)
			d[e[t].to]=d[temp.nd]+e[t].w,q.push(d[e[t].to],(int)e[t].to);
      }
}

inline void add(const vector < int >&fr,const vector < int >&to){
      ++cnt;
      for(register auto f:fr) add(cnt,f,1);
      for(register auto f:to) add(f+T,cnt,0);
}

int main(){
      e.push_back(::E());
      n=qr(1);m=qr(1);k=qr(1);
      build1(1,n,1),build2(1,n,1);
      cnt=T<<1;
      for(register int t=1,t1,t2,t3,t4;t<=m;++t){
	    t1=qr();t2=qr();t3=qr();t4=qr();
	    que(v1,t1,t2,1,n,1);
	    que(v2,t3,t4,1,n,1);
	    add(v1,v2),add(v2,v1);
	    v1.clear();v2.clear();
      }
      que(v1,k,k,1,n,1);
      dij(*v1.begin());
      ans(1,n,1);
      return 0;
}