最长公共子序列模板(LCS)和LICS模板

递归式：

实例图解：

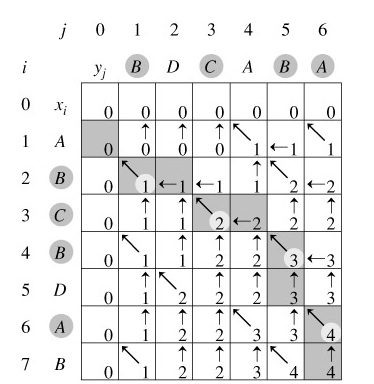
代码：

 #include<stdio.h>
 #include<string.h>
 const int N=;
 int dp[N][N],f[N][N];
 char a[N],b[N],c[N];
 void LCS(char *a,char *b,int la,int lb)
 {
     int i,j;
     memset(dp,,sizeof(dp));
     for(i=;i<=la;i++)
     {
         for(j=;j<=lb;j++)
         {
             if(a[i-]==b[j-])
             {
                 dp[i][j]=dp[i-][j-]+;
                 f[i][j]=;
             }
             else if(dp[i-][j]>dp[i][j-])
             {
                 dp[i][j]=dp[i-][j];
                 f[i][j]=-;
             }
             else
             {
                 dp[i][j]=dp[i][j-];
                 f[i][j]=;
             }
         }
     }
 }
 void dfs(char *s,int i,int j)
 {
     if(!i||!j)  return ;
     if(!f[i][j])
     {
         dfs(s,i-,j-);
         printf("%c",s[i-]);
     }
     if(f[i][j]==)
         dfs(s,i,j-);
     if(f[i][j]==-)
         dfs(s,i-,j);
 }
 int main()
 {
     while(scanf("%s%s",a,b)!=EOF)
     {
         int la=strlen(a),lb=strlen(b);
         LCS(a,b,la,lb);
         printf("%s和%s的最长公共子序列为:\n",a,b);
         dfs(a,la,lb);
         puts("");
         printf("长度为:%d\n",dp[la][lb]);
     }
     return ;
 }

如果不需要记录路径，可以改成一维数组。

 #include<stdio.h>
 #include<string.h>
 const int N=;
 int dp[N];
 char a[N],b[N];
 int LCS(char *a,char *b,int la,int lb)
 {
     int i,j,ma;
     memset(dp,,sizeof(dp));
     for(i=;i<=la;i++)
     {
         ma=;
         for(j=;j<=lb;j++)
         {
             if(dp[j]>ma)    ma=dp[j];
             if(a[i-]==b[j-])
                 dp[j]=ma+;
         }
     }
     for(i=;i<=lb;i++)
         if(dp[i]>ma)
             ma=dp[i];
     return ma;
 }
 int main()
 {
     while(scanf("%s%s",a,b)!=EOF)
     {
         int la=strlen(a),lb=strlen(b);
         printf("长度为:%d\n",LCS(a,b,la,lb));
     }
     return ;
 }

在这个基础上，最长递增(减)子序列（LICS）就可以写了。

 #include<stdio.h>
 #include<string.h>
 const int N=;
 int dp[N];
 int LICS(int *a,int *b,int n,int m)
 {
     int i,j,ma;
     memset(dp,,sizeof(dp));
     for(i=;i<=n;i++)
     {
         ma=;
         for(j=;j<=m;j++)
         {
             if(a[i]>b[j]&&dp[j]>ma)
                 ma=dp[j];
             if(a[i]==b[j])
                 dp[j]=ma+;
         }
     }
     for(i=;i<=m;i++)
         if(dp[i]>ma)
             ma=dp[i];
     return ma;
 }
 int main()
 {
     int a[]={,,,,,};
     int b[]={,,,,,};
     printf("%d\n",LICS(a,b,,));
     return ;
 }

参考文章：http://blog.csdn.net/yysdsyl/article/details/4226630