svd 奇异值分解
参考:http://www.cnblogs.com/pinard/p/6251584.html
酉矩阵,关于矩阵的问题,还是很复杂的。
只有方阵才可以进行特征值分解,
但是如果行不等于列,即不是方阵,还能进行特征值分解吗?
答案是可以的,此时我们的svd登场了。【是不是用奇异值代替了特征值】
奇异值有没有特征值的特性呢???这是一个问题 。
深入理论才行呀。
下面是SVD进行分解的:(它的两边不是对称的)

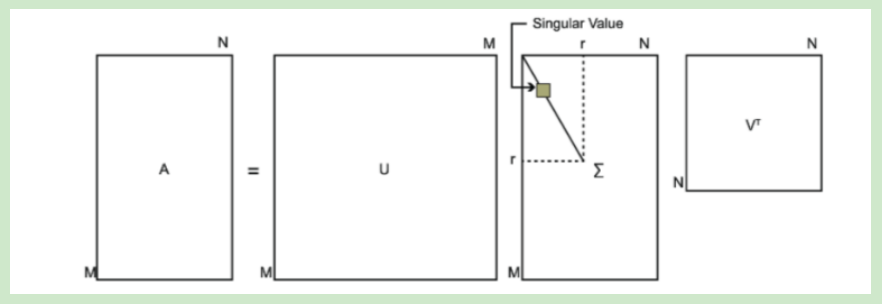
数学就是这样,一些结论记住就好了。(推导太难)
svd 奇异值分解的更多相关文章
- SVD奇异值分解的基本原理和运用
SVD奇异值分解: SVD是一种可靠的正交矩阵分解法.可以把A矩阵分解成U,∑,VT三个矩阵相乘的形式.(Svd(A)=[U*∑*VT],A不必是方阵,U,VT必定是正交阵,S是对角阵<以奇异值 ...
- SVD奇异值分解的几何物理意义资料汇总
学习SVD奇异值分解的网上资料汇总: 1. 关于svd的一篇概念文,这篇文章也是后续几篇文章的鼻祖~ http://www.ams.org/samplings/feature-column/fcarc ...
- [机器学习]-SVD奇异值分解的基本原理和运用
SVD奇异值分解: SVD是一种可靠的正交矩阵分解法.可以把A矩阵分解成U,∑,VT三个矩阵相乘的形式.(Svd(A)=[U*∑*VT],A不必是方阵,U,VT必定是正交阵,S是对角阵<以奇异值 ...
- 『科学计算_理论』SVD奇异值分解
转载请声明出处 SVD奇异值分解概述 SVD不仅是一个数学问题,在工程应用中的很多地方都有它的身影,比如前面讲的PCA,掌握了SVD原理后再去看PCA那是相当简单的,在推荐系统方面,SVD更是名声大噪 ...
- 简单易学的机器学习算法—SVD奇异值分解
简单易学的机器学习算法-SVD奇异值分解 一.SVD奇异值分解的定义 假设M是一个的矩阵,如果存在一个分解: 其中的酉矩阵,的半正定对角矩阵,的共轭转置矩阵,且为的酉矩阵.这样的分解称为M的奇 ...
- 对SVD奇异值分解的理解
首先推荐一篇博客,奇异值分解(SVD)原理详解及推导 - CSDN博客,讲解的很清楚.这里我谈谈自己的理解,方便以后回顾. 如果把向量理解为空间中的一个元素,那么矩阵可以理解为两个空间上的映射 ...
- Deep Learning基础--SVD奇异值分解
矩阵奇异值的物理意义是什么?如何更好地理解奇异值分解?下面我们用图片的例子来扼要分析. 矩阵的奇异值是一个数学意义上的概念,一般是由奇异值分解(Singular Value Decomposition ...
- 机器学习(十七)— SVD奇异值分解
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域.是 ...
- 机器学习降维--SVD奇异值分解
奇异值分解是有着很明显的物理意义,将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性,让机器学会抽取重要的特征,SVD是一个重要的方法. 所以SVD不仅是一个 ...
- SVD奇异值分解
奇异值分解 备忘:Eigen类库可能会和其他库产生冲突,将Eigen类库的头文件引用放到前面解决了.
随机推荐
- android应用开发-从设计到实现 3-9 Origami动态原型设计
动态原型设计 动态的可交互原型产品,是产品经理和界面设计师向开发人员阐释自己设计的最高效工具. 开发人员不须要推測设计师要什么样的效果,照着原型产品做就好了. 非常多创业团队也发现了产品人的这个刚需, ...
- Android底层驱动开发(一)
1 Android为什么要增加硬件抽象层HAL A 统一硬件调用接口.所以利用HAL屏蔽linux驱动的复杂不统一的接口 B 解决GPL版权问题,因为linux内核基于GPL协议.这个G ...
- Fastboot线刷“复活”之刷机心得(三)——错误处理
在刷机的过程中可能不会是一帆风顺的.至少我是这种,总是会遇到这样或者那样的问题,下面是我为大家总结一些问题和解决办法,希望能对大家有所帮助. 一.电量问题 刷机和系统更新有一个共同的前 ...
- 使用bitmap处理海量数据
bitmap是一个十分实用的结构.所谓的Bit-map就是用一个bit位来标记某个元素相应的Value, 而Key即是该元素.因为採用了Bit为单位来存储数据,因此在存储空间方面,能够大大节省. 适 ...
- Mysql第八天 分区与分表
分区表 主要提供例如以下的特性,或者适合如此场景: 数据量非常大, 或者仅仅有表中最后的部分有热点数据.其它均为历史数据 分区表数据更easy维护,能够对独立的分区删除等操作 分区表的数据能够分布在不 ...
- C++ Primer高速入门之六:数组和指针
更新:勘误,delete [] 猪 我们知道,C语言以及早期的面向结构的语言差点儿都支持数组定义.比方整形数组int 女神[2].表示有俩数: 女神[0], 女神[1].她们都是整数. C++ 语言为 ...
- js--09定时器
<!DOCTYPE HTML> <html> <head> <meta http-equiv="Content-Type" content ...
- findFocus-获得拥有焦点的控件
所有的view控件有一个findFocus方法,这个方法如下 /** * Find the view in the hierarchy rooted at this view that current ...
- android 图片特效处理之 图片叠加
这篇将讲到图片特效处理的图片叠加效果.跟前面一样是对像素点进行处理,可参照前面的android图像处理系列之七--图片涂鸦,水印-图片叠加和android图像处理系列之六--给图片添加边框(下)-图片 ...
- How to install Armbian on Orange Pi Plus 2e
bian on Orange Pi Plus 2e How to install Armbian on Orange Pi Plus 2e Armbian on the microSD You jus ...
