[Codeup 25482]选美

[Codeup 25482 ]选美

题目

一年一度的星哥选美又拉开了帷幕

N个人报名参加选拔，每个人都有着各自的相貌参数和身材参数（不大于 10000 的正整数）。你的任务是尽可能让更多人被星哥选中，而唯一要求就是，在这只队伍里面的每个人，都需满足以下不等式：

A (H− h) +B(W− w) ≤ C

其中H和W为这个人的相貌和身材， h和w为选中者中的最小相貌参数和最小身材参数，而A、 B、 C为三个不大于 10000 的正的整型常数。

现在请计算星哥最多可以选中多少人。

INPUT

第一行：一个整数： N(0<N<=2000)

第二行：三个分开的整数： A,B和C

第三行到第N+ 2行：每行有两个用空格分开的整数，分别表示一个人的相貌参数和身材参数

OUTPUT

第一行：最多被选的人数

SAMPLE

INPUT

8

1 2 4

5 1

3 2

2 3

2 1

7 2

6 4

5 1

4 3

OUTPUT

5

解题报告

考试时第一眼看到 星哥 我是茫然的= =，我在想我啥时候还能选美了= =

考试时打了个毫无根据的乱搞暴力，然后貌似竟然还过了一个点

正解：

首先我们观察一下这个式子：

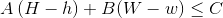
显然可以化简一下，我们先将不等关系改为等于关系，再移项，就可以得到：

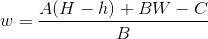
也就是说，我们完全可以得到两个量w与h的等量关系

那么我们想，假如我们知道了其中的h，那么我们一定可以求出这个最小的w，那么我们再把不等关系转回来，我们就得到的最小的w

那么我们就可以得到一个区间  ，只要w在这个区间里，这个人就能被选上（原因很简单，左端点是通过不等关系求出来的，右端点则是它本身的w值，假如最小值大于该值，那么就存在这个Wj比最小值还小，这显然是不成立的，所以显然只有w在该区间里才可以是她被选上）

接下来我们得到了n个区间，我们要让选上的人尽量多，所以我们要求被尽量多的区间所包含的点，来作为我们的w，所以我们可以用差分来处理，左端点+1，右端点后面一个点-1，那么这个点所能满足的数量就是该点的前缀和（差分：我们想为什么这样是可行的，我们只考虑一条线段，在该线段前的点，显然前缀和为0，在该线段中的点，显然前缀和只包含左端点，前缀和为1，在该线段后的点，前缀和中包含的左端点与右端点的1和-1相抵消，故前缀和为0，至于边界，画一画就出来了）

所以只是一个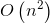求最大前缀和即可，只是常数有点大（人傻自带超大常数）

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 inline int read(){
     int sum();
     char ch(getchar());
     for(;ch<''||ch>'';ch=getchar());
     for(;ch>=''&&ch<='';sum=sum*+(ch^),ch=getchar());
     return sum;
 }
 int n,a,b,c;
 int H[],W[];
 int sum[];
 int tp(),ans();
 int main(){
     n=read(),a=read(),b=read(),c=read();
     for(int i=;i<=n;i++)
         H[i]=read(),W[i]=read(),tp=max(tp,W[i]);
     for(int i=;i<=n;i++){
         memset(sum,,sizeof(sum));
         for(int j=;j<=n;j++)
             if(H[j]>=H[i]&&a*(H[j]-H[i])<=c){
                 int tmp((a*(H[j]-H[i])+b*W[j]-c)/b);
                 if(tmp<)
                     tmp=;
                 if(tmp>W[j])
                     tmp=W[j];
                 sum[tmp]++,sum[W[j]+]--;
             }
         for(int j=;j<=tp;j++)
             sum[j]+=sum[j-];
         for(int j=;j<=n;j++)
             if(H[j]>=H[i]&&a*(H[j]-H[i])<=c)
                 ans=max(ans,sum[W[j]]);
     }
     printf("%d",ans);
 }