机器学习基石10-Logistic Regression

注：
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程。
笔记原作者：红色石头
微信公众号：AI有道

上一节课介绍了Linear Regression线性回归，用均方误差来寻找最佳的权重向量\(w\)，获得最好的线性预测。本节课将介绍Logistic Regression逻辑回归问题。

一、Logistic Regression Problem

一个心脏病预测的问题：根据患者的年龄、血压、体重等信息，来预测患者是否会有心脏病。很明显这是一个二分类问题，其输出\(y\)只有\({0,1}\)两种情况。

二元分类，一般情况下，理想的目标函数\(f(x)>0.5\)，则判断为正类\(1\)；若\(f(x)<0.5\)，则判断为负类\(-1\)。

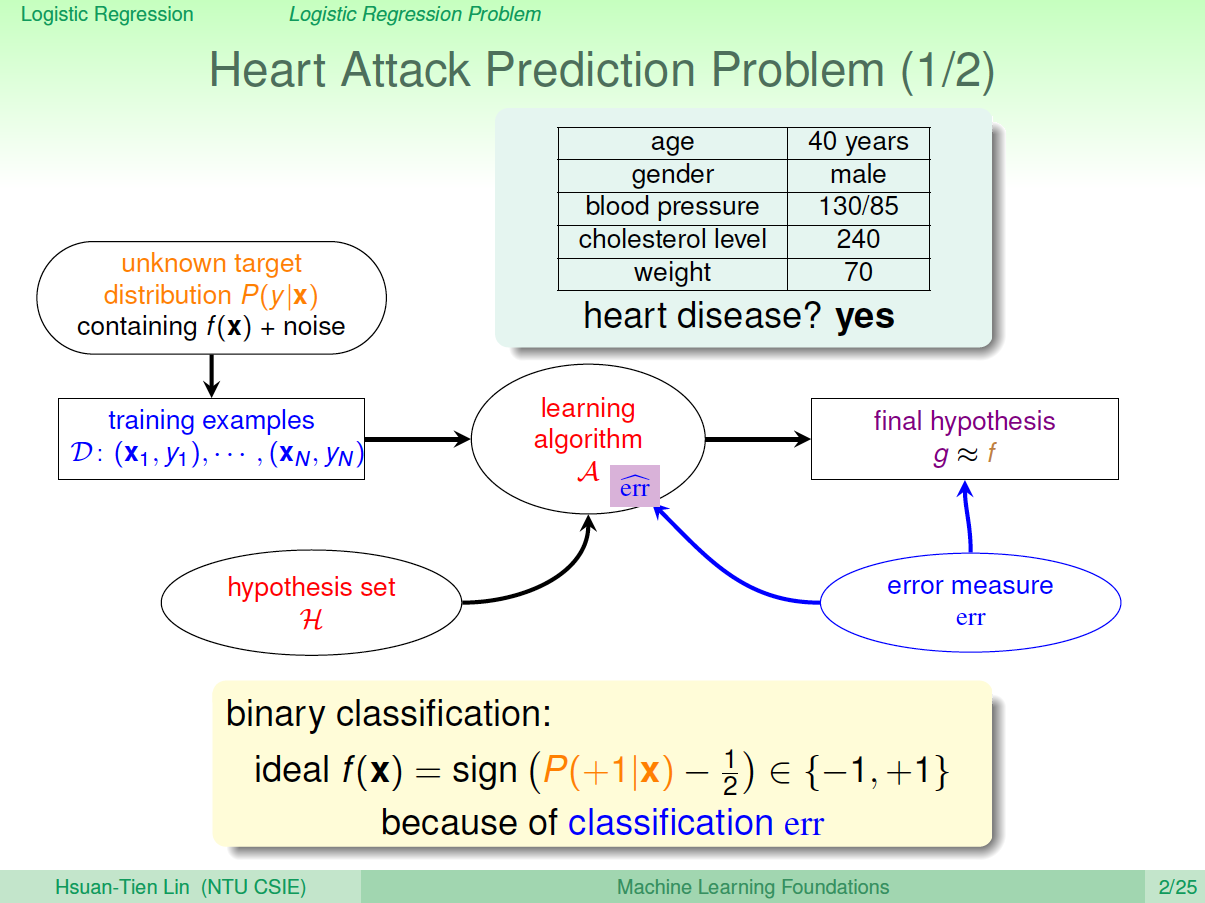
但是，如果我们想知道的不是患者有没有心脏病，而是到底患者有多大的几率是心脏病。这表示，我们更关心的是目标函数的值（分布在0,1之间），表示是正类的概率（正类表示是心脏病）。这跟我们原来讨论的二分类问题不太一样，我们把这个问题称为软性二分类问题（'soft' binary classification）。这个值越接近\(1\)，表示正类的可能性越大；越接近\(0\)，表示负类的可能性越大。

对于软性二分类问题，理想的数据是分布在\([0,1]\)之间的具体值，但是实际中的数据只可能是\(0\)或者\(1\)，我们可以把实际中的数据看成是理想数据加上了噪声的影响。

如果目标函数是\(f(x)=P(+1|x)\in[0,1]\)的话，我们如何找到一个好的Hypothesis跟这个目标函数很接近呢？
首先，根据我们之前的做法，对所有的特征值进行加权处理。计算的结果为\(s\)，我们称之为'risk score'：

但是特征加权和\(s\in (-\infty,\infty)\)，如何将\(s\)值限定在\([0,1]\)之间呢？一个方法是使用sigmoid Function，记为\(\theta(s)\)。那么我们的目标就是找到一个hypothesis \(h(x)=\theta(w^Tx)\)。

Sigmoid Function函数记为\(\theta(s)=\frac{1}{1+e^{-s}}\)，满足\(\theta(-\infty)=0\)，\(\theta(0)=\frac{1}{2}\) ，\(\theta(+\infty)=1\)。这个函数是平滑的、单调的S型函数。

对于逻辑回归问题，hypothesis就是这样的形式：\[h(x)=\frac{1}{1+e^{-w^Tx}}\]我们的目标就是求出这个预测函数\(h(x)\)，使它接近目标函数\(f(x)\)。

二、Logistic Regression Error

现在我们将Logistic Regression与之前讲的Linear Classification、Linear Regression做个比较

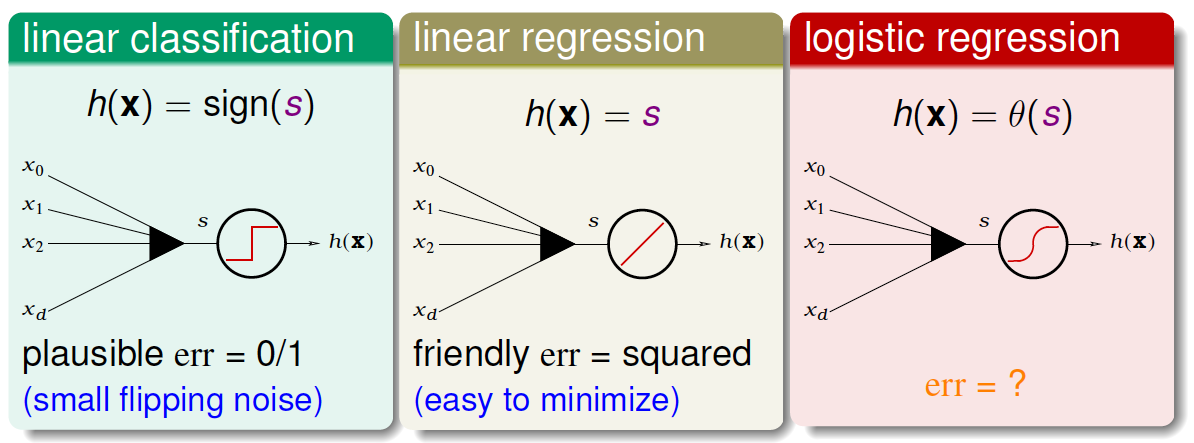
这三个线性模型都会用到线性score function \(s=w^Tx\)。linear classification的误差使用的是0/1 err；linear regression的误差使用的是squared err。那么logistic regression的误差该如何定义呢？

先介绍一下“似然性”的概念。目标函数\(f(x)=P(+1|x)\)，如果我们找到了一个hypothesis很接近target function。也就是说，在所有的Hypothesis集合中找到一个hypothesis与target function最接近，能产生同样的数据集D，包含\(y\)输出label，则称这个hypothesis是最大似然likelihood。

logistic function: \(h(x)=\theta(w^Tx)\)满足一个性质：\(1-h(x)=h(-x)\)，所以\[likelihood(h)=P(x_1)h(+x_1)\times P(x_2)h(-x_2)\times ... P(x_N)h(-x_N)\]
因为\(P(x_n)\)对所有的\(h\)来说，都是一样的，所以我们可以忽略它。那么我们可以得到logistic \(h\)正比于所有的\(h(y_nx_n)\)乘积。我们的目标就是让乘积值最大化。

如果将\(w\)代入的话：

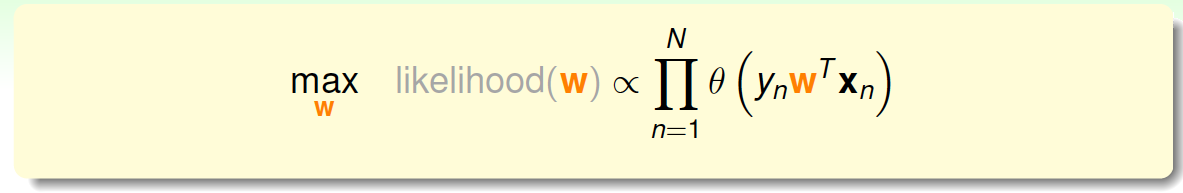
为了把连乘问题简化计算，我们可以引入\(ln\)操作，让连乘转化为连加：

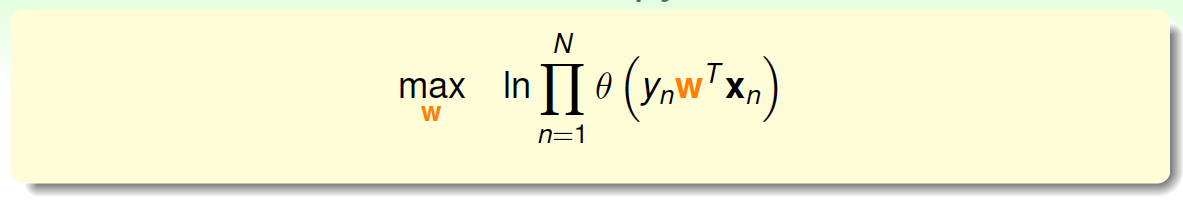
接着，我们将maximize问题转化为minimize问题，添加一个负号就行，并引入平均数操作\(\frac{1}{N}\)：

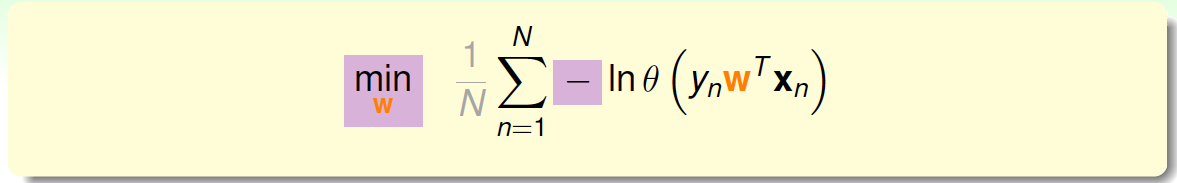
将logistic function的表达式带入，那么minimize问题就会转化为如下形式：

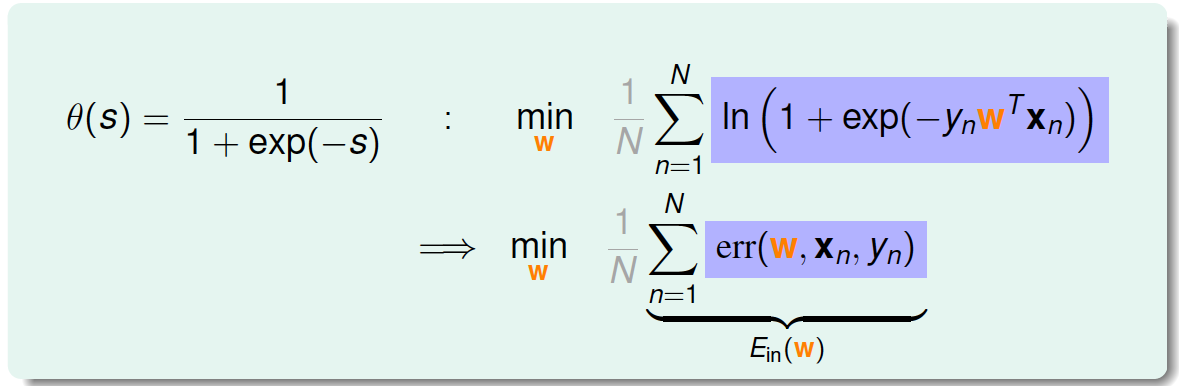
至此，我们得到了logistic regression的err function，称之为cross-entropy error交叉熵误差：

三、Gradient of Logistic Regression Error

我们已经推导了\(E_{in}\)的表达式，那接下来的问题就是如何找到合适的向量\(w\)，让\(E_{in}\)最小。

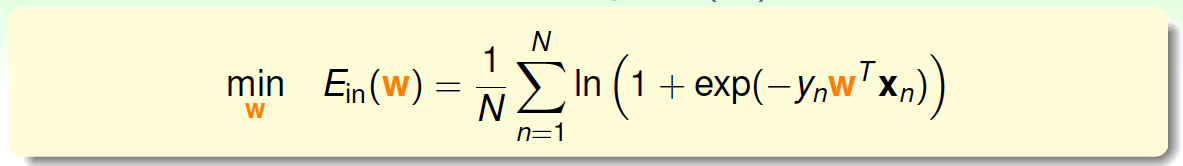
Logistic Regression的\(E_{in}\)是连续、可微、二次可微的凸曲线（开口向上），根据之前Linear Regression的思路，我们只要计算\(E_{in}\)的梯度为零时的\(w\)，即为最优解。

对\(E_{in}\)计算梯度：

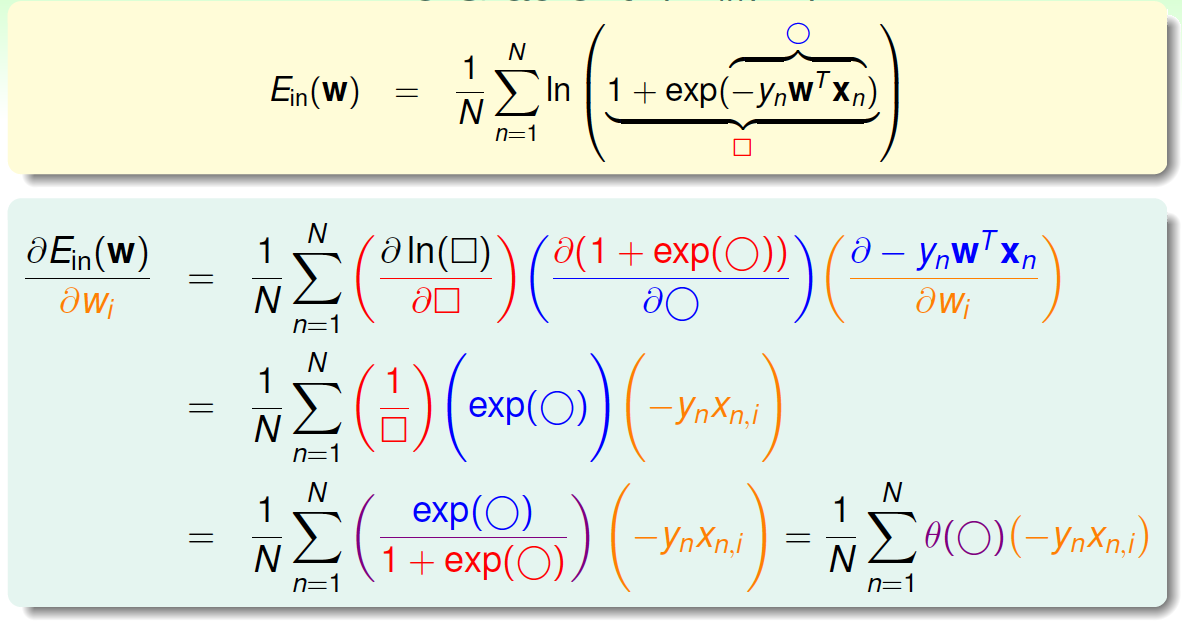
最终得到梯度的表达式为：

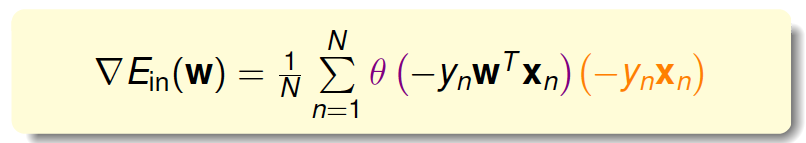
为了计算\(E_{in}\)最小值，我们就要找到让\(\nabla E_{in}(w)\)等于0的位置。

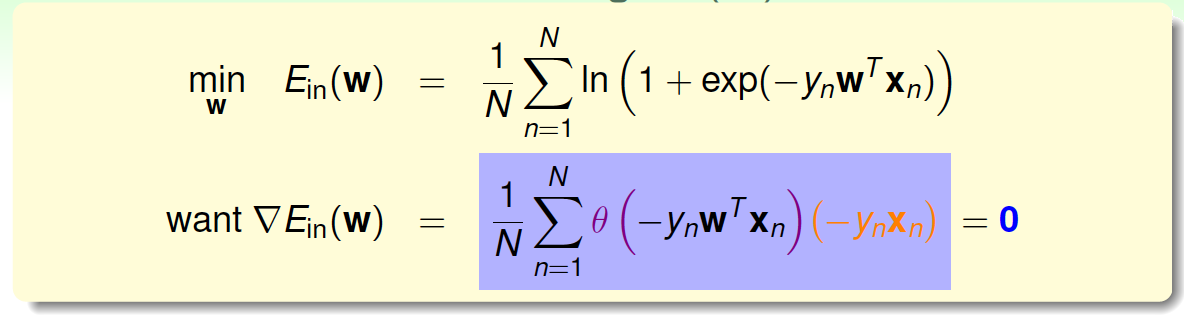
上式可以看成\(\theta(-y_nw^Tx_n)\)是\(-y_nx_n\)的线性加权。要求\(\theta(-y_nw^Tx_n)\)与\(-y_nx_n\)的线性加权和为0，那么一种情况是线性可分，这是因为如果所有的权重\(\theta(-y_nw^Tx_n)\)为0，那就能保证\(\nabla E_{in}(w)\)为\(0\)。\(\theta(-y_nw^Tx_n)\)是sigmoid function，根据其特性，只要让\(-y_nw^Tx_n\ll 0\)，即\(y_nw^Tx_n\gg 0\)。\(y_nw^Tx_n\gg 0\)表示对于所有的点， \(y_n\)与\(w^Tx_n\)都是同号的，这表示数据集D必须是全部线性可分的才能成立。

然而，保证所有的权重为0是不太现实的，总有不等于0的时候，那么另一种常见的情况是非线性可分，只能通过使加权和为零，来求解\(w\)。这种情况没有closed-form解，与Linear Regression不同，只能用迭代方法求解。

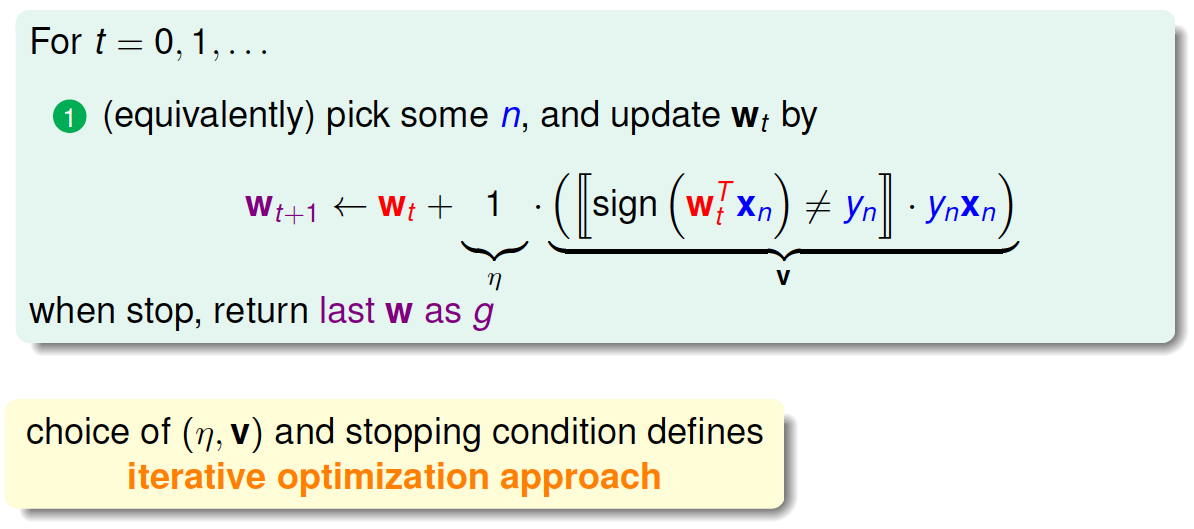
之前所说的Linear Regression有closed-form解，可以说是“一步登天”的；但是PLA算法是一步一步修正迭代进行的，每次对错误点进行修正，不断更新\(w\)值。PLA的迭代优化过程表示如下：

\(w\)每次更新包含两个内容：一个是每次更新的方向\(y_nx_n\)，用\(v\)表示，另一个是每次更新的步长\(\eta\)。参数\((v,\eta)\)和终止条件决定了我们的迭代优化算法。

四、Gradient Descent

根据上一节PLA的思想，迭代优化让每次\(w\)都有更新：

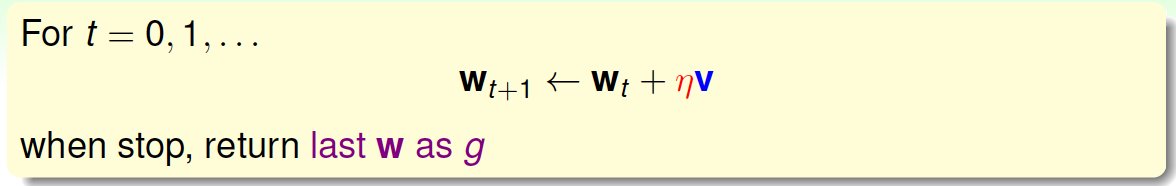
我们把曲线\(E_{in}(w)\)看做是一个山谷的话，要求\(E_{in}(w)\)最小，即可比作下山的过程。整个下山过程由两个因素影响：一个是下山的单位方向\(v\)；另外一个是下山的步长\(\eta\)。

利用微分思想和线性近似，假设每次下山我们只前进一小步，即\(\eta\)很小，那么根据泰勒Taylor一阶展开，可以得到：\[E_{in}(w_t+\eta v)\approx E_{in}(w_t)+\eta v^T \nabla E_{in}(w_t)\]
迭代的目的是让\(E_{in}\)越来越小，即让\(E_{in}(w_t+\eta v)<E_{in}(w_t)\)。\(\eta\)是标量，如果两个向量方向相反的话，那么他们的内积最小（为负），也就是说如果方向\(v\)与梯度\(\nabla E_{in}(w_t)\)反向的话，那么就能保证每次迭代\(E_{in}(w_t+\eta v)<E_{in}(w_t)\)都成立。因此我们令下降方向为：\[v=-\frac{\nabla E_{in}(w_t)}{\|\nabla E_{in}(w_t)\|}\]
\(v\)是单位向量， \(v\)每次都是沿着梯度的反方向走，这种方法称为梯度下降（gradient descent）算法。那么每次迭代公式就可以写成：\[w_{t+1} = w_t-\eta \frac{\nabla E_{in}(w_t)}{\|\nabla E_{in}(w_t)\|}\] 下面讨论一下\(\eta\)的大小对迭代优化的影响： \(\eta\)如果太小的话，那么下降的速度就会很慢； \(\eta\)如果太大的话，那么之前利用Taylor展开的方法就不准了，造成下降很不稳定，甚至会上升。因此，\(\eta\) 应该选择合适的值，一种方法是在梯度较小的时候，选择小的\(\eta\)，梯度较大的时候，选择大的\(\eta\)，即正比于\(\|\nabla E_{in}(w_t)\|\)。这样保证了能够快速、
稳定地得到最小值\(E_{in}(w)\)。

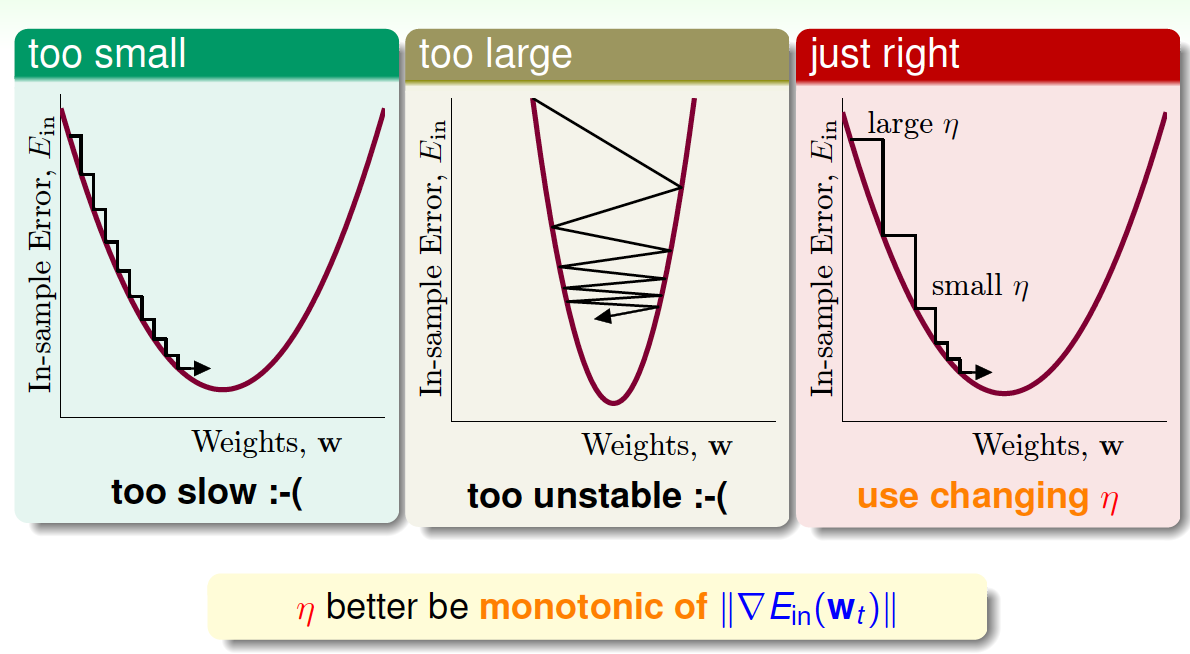
对学习速率\(\eta\)做个更修正，梯度下降算法的迭代公式可以写成：\[w_{t+1} = w_t-\eta' \nabla E_{in}(w_t)\]
其中\[\eta'=\frac{\eta}{\|\nabla E_{in}(w_t)\|}\]
总结一下基于梯度下降的Logistic Regression算法步骤如下：

• 初始化\(w_0\)
• 计算梯度\(\nabla E_{in}(w_t)=\frac{1}{N}\sum^N_{n=1}\theta(-y_nw^T_tx_n)(-y_nx_n)\)
• 迭代更新\(w_{t+1} = w_t-\eta' \nabla E_{in}(w_t)\)
• 满足\(\nabla E_{in}(w_{t+1})\approx 0\) 或者达到迭代次数，迭代结束

五、总结

我们今天介绍了Logistic Regression。首先，从逻辑回归的问题出发，将\(P(+1|X)\)作为目标函数，将\(\theta(w^Tx)\)作为hypothesis。接着，我们定义了logistic regression的err function，称之为cross-entropy error交叉熵误差。然后，我们计算logistic regression error的梯度，最后，通过梯度下降算法，计算\(\nabla E_{in}(w_{t+1})\approx 0\) 时对应的\(w_t\)值。