EOJ Monthly 2019.2 题解(B、D、F)

EOJ Monthly 2019.2 题解(B、D、F)

官方题解：https://acm.ecnu.edu.cn/blog/entry/320/

B. 解题

单测试点时限: 2.0 秒

内存限制: 1024 MB

“我把房门上锁，并非为了不让她进去，而是为了防止自己逃到她身边”。

她又被数学难住了。QQ 小方当然是不会对女生说”不”的。

她的数学题是这样的，她得到了一个十进制大整数，这个大整数只包含 1 - 9 这 9 个数字。

现在，要求选出其中连续的一段数字，把其他未被选中的数字全部变成 0，并且使得变换以后的大整数恰好是 m 的倍数。

QQ 小方为了表现自己的能力，所以一口答应给她写出在所有可能的数里面最小的一个。

但是她的问题太多了，她对于这一个大整数，需要对于 q 个不尽相同的 m 分别给出答案。

但是 QQ 小方自己不会。只能来求助你了，你能帮他解答吗？

输入

第一行包含一个大整数，这个整数的位数为 n (1≤n≤10⁶)。

第二行一个整数 q (1≤q≤500) 代表询问次数。

对于每一个询问，包含一行一个整数，表示第 i 次询问的 mi (1≤m_i≤5×10⁷)。

保证 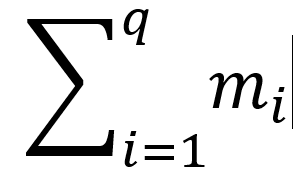  ≤5×10⁷ 。

输出

对于每一个询问输出两个整数 l,r 表示保留第 l 到第 r 位。保证一定有解。

样例

input

1249
4
7
3
2
83

output

3 4
4 4
3 3
2 4

提示

对于样例：
1249 这个数中，可选出的最小的7的倍数是49，最小的3的倍数是9，2的倍数是40，83的倍数是249。

题解：

对于该题，很明显可以想到对于所有的可能的解一定可以写成：a_i - a_j  的形式，设 a_i 是从第 i 位到末位代表的整数。

n是一个大整数，显然a_i 不能完全表示具体的数，而若a_i - a_j ≡0(mod m)可以得出a_i % m = a_j % m，而如何让这个答案a_i - a_j 最小呢？就要使得a_i 越小，a_j 越大就好，就是i越靠近后面，j是从末尾到i的所有a[j]中最靠近i的,显然a[j]要从最后面一位+1开始枚举，因为比如说答案是最后一位，那么i=len(整个长度)，j=len+1，所以i要从len开始往前枚举，j再从len+1枚举到i+1。

这就是大概的思路，然后，如果像上述的方法去做，时间就变成了预处理len次，枚举len² ，时间就变成了o(len+len²)，len就是n，n最多为1e6，显然会超时。

其实对于mod m，根据鸽巢原理(抽屉原理)，你最多枚举m+1次我就能找到两个相同的a[i]和a[j]，然后找a[i]和a[j] 时，我们可以这样，先从a[len+1]开始往前枚举，如果枚举到某个a[i]，发现这个数已经出现过了，那么这就是我们想要的答案，这样你在找可以边找处理a[i]，就可以边找答案，最多处理m+1次，这样就不会超时。具体看代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+;
const int maxm=5e7+;
int n,m,t;
char s[maxn];
int a[maxn];
struct node{
    int num;
    int have;
}vis[maxm];
int main(){
    int len=;
    char c;
    while(c=getchar()){
        if(c>='' && c<='') s[len++]=c;
        else{
            s[len]='\0';
            break;
        }
    }
    len--;
    scanf("%d",&t);
    while(t--){
        scanf("%d",&m);
        for(int i=; i<=m; i++){
            vis[i].num=;
            vis[i].have=;
        }
        a[len+]=;
        vis[a[len+]].num=len+;
        vis[a[len+]].have=;
        int tmp=;
        for(int i=len; i>&&i>=len-m; i--){
            a[i]=((s[i]-'')*tmp+a[i+])%m;
            tmp=(tmp*)%m;
            if(vis[a[i]].have==){
                vis[a[i]].num=i;
                vis[a[i]].have=;
            }
            else{
                printf("%d %d\n",i,vis[a[i]].num-);
                break;
            }
        }
    }
}

D. 进制转换

单测试点时限: 2.0 秒

内存限制: 256 MB

“他觉得一个人奋斗更轻松自在。跟没有干劲的人在一起厮混，只会徒增压力。”

QQ 小方决定一个人研究研究进制转换。

很快，QQ 小方就遇到问题了。他现在想知道在十进制范围 [l,r] 内有多少整数满足在 k 进制下末尾恰好有 m 个 0。

比如在十进制下的 24 在二进制下是 11000，我们称十进制下的 24 在二进制下末尾恰好有 3 个 0。

QQ 小方一筹莫展，你能帮他解决问题吗？

输入

第一行包含一个整数 T (1≤T≤10⁵) 表示数据组数。

对于每组数据包含一行，四个整数 l,r,k,m ( 1≤l≤r≤10¹⁸, 2≤k,m≤100)，含义如题目所述。

输出

对于每组数据输出一行，包含一个整数，表示答案。

样例

input

2
1 10 2 3
1 100 2 3

output

1
6

提示

例如，在 100 进制下，末位是 90 的数不算作有末尾 0。

题解：

 

题目要求的时在区间范围内的m进制后有k个零的数有多少，很容易想到如果一个数的m进制后有k个零，就一定能被m^k  整除，而在含k个零中，一定存在含k+1个零的（含k+1个零就意味着一定含k个零），在1，2，3....x中，能被m^k  整除的有⌊x/m^k⌋个，所以只含k个零的个数有ans_x = ⌊x/m^k⌋-⌊x/m^k+1⌋，区间的话就是ans_r - ans_l-1 注意是l-1

但是有个问题，就是直接计算m^k 会溢出的问题，而且又不能取模，根据式子，就要用到除法，如果溢出了，相除肯定变成了0（据说long double好像也行，我没试过）

#include<bits/stdc++.h>
using namespace std;
typedef long long llx;
llx t,l,r,k,m;
int main(){
    cin>>t;
    while(t--){
        cin>>l>>r>>k>>m;
        l--;
        llx ll=l,rr=r;
        for(llx i=; i<m; i++){
            rr=(llx)(rr/k);
            ll=(llx)(ll/k);
        }
        llx rrr=(llx)(rr/k);
        llx lll=(llx)(ll/k);
        cout<<rr-ll-rrr+lll<<endl;
    }
}

 

F. 方差

单测试点时限: 2.0 秒

内存限制: 256 MB

“放弃不难，但坚持一定很酷。”

QQ 小方已经在体育馆苦练一天射箭了，但他还在坚持。

QQ 小方每天都要在朋友圈晒自己的训练记录。他一共进行了 n 次射箭，成绩分别是 x1,x2,⋯,xn。为了表现自己的发挥十分稳定，QQ 小方决定选出其中的 m 次成绩，使得他们的方差是所有可以选择的方案中最小的。

对于 m 个元素组成的数列 a1,a2,⋯,am，我们知道他们的方差 σ2=(a1−a¯)2+(a2−a¯)2+⋯+(am−a¯)2m ，其中 a¯=a1+a2+⋯+amm。

但是这个问题对 QQ 小方来说太难了，你需要去帮助 QQ 小方。

为了方便，现在你需要输出这个最小的 σ2 乘以 m2 以后的结果。

输入

输入一行包含两个正整数 n (1≤n≤106) 和 m (1≤m≤n)。接下来一行包含 n 个整数 x1,x2,⋯,xn (1≤xi≤103)。

输出

输出一行包含一个整数，表示答案。为了方便，我们需要输出最小的 σ2 乘以 m2 以后的结果。

样例

input

5 3
1 2 3 4 5

output

6

题解：

这题就是公式的变形

（=_=）直接看上面的题解吧，注意用long long。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn=1e6+;
ll a[maxn],sum1[maxn],sum2[maxn];
int main(){
    ll n,m;
    scanf("%lld %lld",&n,&m);
    for(ll i=; i<=n; i++) scanf("%lld",&a[i]);
    sort(a+,a+n+);
    for(ll i=; i<=n; i++){
        sum1[i]=sum1[i-]+a[i];
        sum2[i]=sum2[i-]+a[i]*a[i];
    }
    ll minn=LONG_LONG_MAX;
    for(ll i=m; i<=n; i++){
        ll tmp=(sum2[i]-sum2[i-m])*m-(sum1[i]-sum1[i-m])*(sum1[i]-sum1[i-m]);
        minn=min(minn,tmp);
    }
    printf("%lld\n",minn);
}