【题解】Luogu CF86D Powerful array
原题传送门
裸的莫队啊,我博客里有对莫队较详细的介绍
这道题很简单,可以说是裸的模板
但是如何在已有的值上进行操作?
小学生应该都知道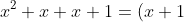^2)
那么转移就超级简单了qaq
inline void add(register int c)
{
sum+=(num[c]+num[c]+1)*c;
++num[c];
}
inline void del(register int c)
{
--num[c];
sum-=(num[c]+num[c]+1)*c;
}
要开long long(虽说我没试过int,但我觉得会炸int)
#include <bits/stdc++.h>
#define N 200005
using namespace std;
inline int read()
{
register int x=0,f=1;register char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
inline void write(register long long x)
{
if(!x)putchar('0');if(x<0)x=-x,putchar('-');
static int sta[25];int tot=0;
while(x)sta[tot++]=x%10,x/=10;
while(tot)putchar(sta[--tot]+48);
}
struct query{
int l,r,id,bl;
}q[N];
int a[N],blocksize=0,num[1000005];
long long ans[N],sum=0;
inline void add(register int c)
{
sum+=(num[c]+num[c]+1)*c;
++num[c];
}
inline void del(register int c)
{
--num[c];
sum-=(num[c]+num[c]+1)*c;
}
inline bool cmp(register query a,register query b)
{
return a.bl!=b.bl?a.l<b.l:(a.bl&1?a.r<b.r:a.r>b.r);
}
int main()
{
int n=read(),m=read();
blocksize=sqrt(n);
for(register int i=1;i<=n;++i)
a[i]=read();
for(register int i=1;i<=m;++i)
{
int l=read(),r=read();
q[i]=(query){l,r,i,(l-1)/blocksize+1};
}
sort(q+1,q+1+m,cmp);
int l=1,r=0;
for(register int i=1;i<=m;++i)
{
int ll=q[i].l,rr=q[i].r;
while(ll<l)
add(a[--l]);
while(ll>l)
del(a[l++]);
while(rr>r)
add(a[++r]);
while(rr<r)
del(a[r--]);
ans[q[i].id]=sum;
}
for(register int i=1;i<=m;++i)
write(ans[i]),printf("\n");
return 0;
}
【题解】Luogu CF86D Powerful array的更多相关文章
- CF86D Powerful array
题意翻译 题意:给出一个n个数组成的数列a,有t次询问,每次询问为一个[l,r]的区间,求区间内每种数字出现次数的平方×数字的值 的和. 输入:第一行2个正整数n,t. 接下来一行n个正整数,表示数列 ...
- CodeForces - 86D D. Powerful array —— 莫队算法
题目链接:http://codeforces.com/problemset/problem/86/D D. Powerful array time limit per test 5 seconds m ...
- CodeForces 86 D Powerful array 莫队
Powerful array 题意:求区间[l, r] 内的数的出现次数的平方 * 该数字. 题解:莫队离线操作, 然后加减位置的时候直接修改答案就好了. 这个题目中发现了一个很神奇的事情,本来数组开 ...
- Codeforces 86D Powerful array (莫队)
D. Powerful array time limit per test 5 seconds memory limit per test 256 megabytes input standard i ...
- CodeForces 86D Powerful array(莫队+优化)
D. Powerful array time limit per test 5 seconds memory limit per test 256 megabytes input standard i ...
- D. Powerful array 莫队算法或者说块状数组 其实都是有点优化的暴力
莫队算法就是优化的暴力算法.莫队算法是要把询问先按左端点属于的块排序,再按右端点排序.只是预先知道了所有的询问.可以合理的组织计算每个询问的顺序以此来降低复杂度. D. Powerful array ...
- codefroce D. Powerful array[初识块状数组]
codefroce D. Powerful array[初识块状数组] 由于是初始所以,仅仅能先用别人的分析.囧... 题目: 给定一个数列:A1, A2,--,An,定义Ks为区间(l,r)中s出现 ...
- D. Powerful array
D. Powerful array 题意 给定一个数列:a[i] (1<= i <= n) K[j]表示 在区间 [l,r]中j出现的次数.有t个查询,每个查询l,r,对区间内所有a[i] ...
- Yandex.Algorithm 2011 Round 2 D. Powerful array 莫队
题目链接:点击传送 D. Powerful array time limit per test 5 seconds memory limit per test 256 megabytes input ...
随机推荐
- [Java in NetBeans] Lesson 02. Variables, Data Types and Assignment.
这个课程的参考视频在youtube. 主要学到的知识点有: Data Type: int, char, String, double, boolean. When into printf, int ( ...
- \Temporary ASP.NET Files\root\文件不断增长,如何处理?
很久没有写博了.最近半年除了忙活布置新家和过年期间走亲访友之外,都是在公司处理一些项目中的杂事:连家里买的很多书都停下来没看了,感觉这段时间在事业和学习上一直都是忙忙碌碌,却又碌碌无为. 吐槽完,说正 ...
- Adobe Acrobat 9 Pro序列号
其实只删除c:\Program Files\Common Files\Adobe\Adobe PCD\cache目录下的cache.db文件也是可以的,然后重新打开Adobe ,输入序列号1118-4 ...
- Elasticsearch5.x批量插入数据(Java)
先上官方示例代码:官方示例 Java代码: // 批量插入数据 public void InsertBatch() { try { // 设置集群名称 Settings settings = Sett ...
- sql server相关
sql server nolock 在sqlserver 中with(nolock)详解 所有Select加 With (NoLock)解决阻塞死锁 在查询语句中使用 NOLOCK 和 READP ...
- python class 1
//test.py class Employee: 'all employee' empCount = 0 def __init__(self, name, salary): self.name = ...
- iOS UI基础-13.0 数据存储
应用沙盒 每个iOS应用都有自己的应用沙盒(应用沙盒就是文件系统目录),与其他文件系统隔离.应用必须待在自己的沙盒里,其他应用不能访问该沙盒 应用沙盒的文件系统目录,如下图所示(假设应用的名称叫Lay ...
- Linux之HugePages快速配置
关于Linux系统的HugePages与Oracle数据库优化,可以参考熊爷之前的文章,相关概念介绍的非常清晰: Linux大内存页Oracle数据库优化 本文旨在Linux系统上快速配置HugePa ...
- Unity shader学习之折射
shader如下: Shader "Custom/Refraction" { Properties { _Cubemap("Cubemap", Cube) = ...
- Python之words count
要求: 对文件单词进行统计,不区分大小写,并显示单词重复最多的十个单词 思路: 利用字典key,value的特性存单词及其重复的次数 每行进行特殊字符的处理,分离出被特殊字符包含的单词 def mak ...
