【hihoCoder】1033: 交错和

初探数位dp 介绍了数位类统计的基础知识。以下列出其中的基础点：

基本问题

统计在区间[l, r]中满足条件的数的个数

思路

1. [l, r] 将问题转换为 在[0, r]中满足条件的个数 - 在[0, l)满足条件的个数

2. 求解 区间[0, n]满足条件的个数

• 性质：一个小于n的数m，一定是从高位到低位在某一位小于n的对应位的一个数

	数值	百位	十位	个位
n	358	3	5	8
m	350	3	5	0	0<8
m	349	3	4	9	4<5

• 遍历所有小于n的数：从高位到低位枚举第一次小于n的数位，之后数位的值就不受限制了

	数值	百位	十位	个位
n	358	3	5	8
m		3	4	0...9
m		2	0...9	0...9

• 遍历可以构成一棵树，类似深度优先遍历。第一个图是小于35的数，第二个图是一般情况，i+1的数位比i的大

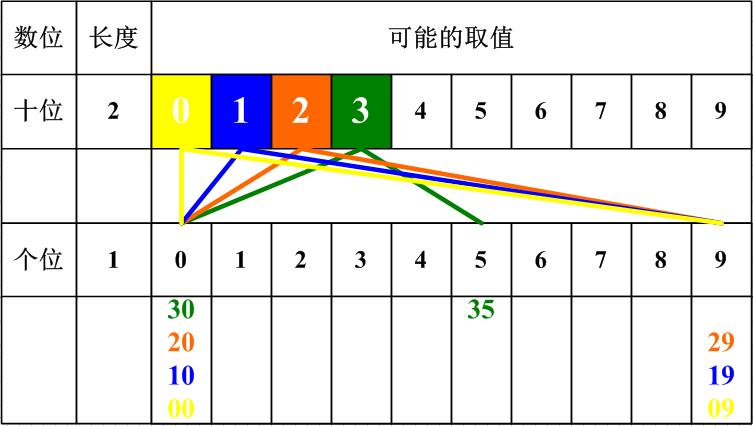
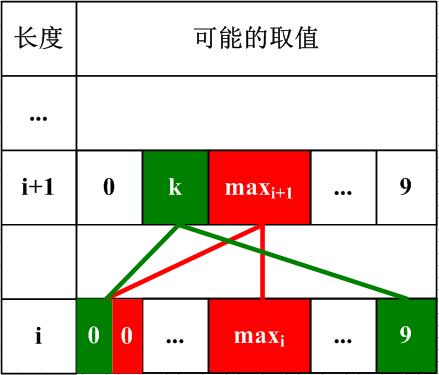
• 递归计算区间[0,n]中满足条件的数

数位	i	i-1	...
数位上的值	digit	digit' 0...可以取的最大值	...

F[i, digit, st]表示长度为i，第i位的位为digit，且满足条件st的数的个数。F[i, digit, st] = F[i, digit, st] + F[i-1, digit', st']

• 动态规划：函数的参数表明了一个状态

 void dp(int 当前数的长度len, int 当前数位的值 digit, bool 当前数前面数位都是0 begin_zero, bool 下一个数位的值有限制 islimit)
 {
     if(len == )//当前数的长度为1
     {    ...//直接讨论返回
           return;
     }
     //遍历下一位的所有取值情况
     int maxValue = (islimit?n[len]:);//下一位的最大取值
     for(int i = ; i <= maxValue; i++)
     {
          bool _begin_zero = (i ==  && begin_zero);
          bool _islimit = (i == maxValue);
          dp(len - , i, _begin_zero, _islimit);
      }
 }

Tips:

• 假设区间[0, n]中n的位数为 len(n)，初始要从len(n)+1开始。这样对第len(n)位讨论的时候就可以和其它位一样。
• 计算过程中，只有当数位的值没有限制时才把结果存入F[i, digit, st]中，否则会缺失一些结果
• 前面的数位都为0和不全为0需要作为两种状态存储

源码 http://hihocoder.com/problemset/problem/1033

 #include<iostream>
 using namespace std;

 #define ll long long int //需要用long long 来进行存放
 const int mod = ;//结果的最大值，用于取模
 struct node{
     ll s, n;//s: 各数位交错和 n：满足条件的个数
 };
 node dp[][][];//[长度][以哪个数作为开头][该数的数位交错和]
 int bits[];//存放一个数的各位，低到高存放在0到20
 ll base[];//每一数位的基准 比如十位数=base[2]=10

 //len数位长度, dig是首个数字, begin_zero表示从最高位到当前位是否全部为0， limit表示下一位枚举是否有限制（bit[len-2]或9）， sum是要求的数字和
 node dfs(int len, int dig, bool begin_zero, bool limit, int sum){
     node t;//存放长度为 len的结果
     t.s = , t.n = ;
     //超过边界值
     if (len <=  || len >=  || dig <  || dig >  || sum < - || sum >= )
         return t;
     //返回已有的DP结果，即记忆化搜索
     if (!limit && dp[len][dig + (begin_zero ?  : )][sum + ].n != -)
         return dp[len][dig + (begin_zero ?  : )][sum + ];
     //长度只有一位，就不需要枚举下一位了，直接讨论返回即可
     if (len == ){
         if (dig != sum)
             return t;
         t.n = , t.s = sum;
         return t;
     }
     //开始枚举下一位的数字
     int end = limit ? bits[len - ] : ;//下一位数字的最大值
     int newsum = dig - sum;
     node tmp;
     for (int j = ; j < end + ; j++)
     {
         if (begin_zero){//前面都是0，接下来的就由当前位决定 j是否为0
             tmp = dfs(len - , j, j == , limit && (j == end), sum);
         }
         else{//前面不是全为0
             tmp = dfs(len - , j, false, limit && (j == end), newsum);
         }
         //将tmp的值累加到t上
         t.n += tmp.n;//满足条件的个数
         //计算满足条件的长度为 len 的data[len]所有数的和， tmp 是长度为 i-1的data[len-1]所有数的和
         //每一个： data[len] = dig * base[len] + data[len-1]  且共有n个
         //t.s = t.s + tmp.n * (dig * base[len]) + tmp.s 增加 %mod 就得到下面的结果
         t.s = ((t.s + tmp.s) % mod + ((tmp.n * dig) % mod * base[len]) % mod) % mod;
     }
         //当长度为len，且以dig开头的，数位和为sum 的所有结果都计算完成，才将其进行存储
     if (!limit)
         dp[len][dig + (begin_zero ?  : )][sum + ] = t;
         //dig + (begin_zero ? 0 : 10) 用来区分两种状态，（1. 前导都为0；2. 前导包含其它数）
     return t;
 }

 int solve(ll n, int s){
     if (n <= )
         return ;
     int l = ;
     for (int i = ; i < ; i++)
         bits[i] = ;
     //将n的每一位从低到高放到 bits[0]到bits[l] 中
     while (n){
         bits[l++] = n % ;
         n /= ;
     }
     //从l+1开始，比n的长度大1，并且第l+1位数置为0
     return  dfs(l + , , true, true, s).s;
 }

 int main(){
     ll l, r, s;
     node t;
     t.n = -;
     t.s = ;
     for (int i = ; i < ; i++)//长度
         for (int j = ; j < ; j++)//第i位的取值
             for (int k = ; k < ; k++)// i到0 所有位上的交错和 + 200
                 dp[i][j][k] = t;
     base[] = ;
     for (int i = ; i < ; i++)//base 是作为基准数 比如两位数需要 *10, 三位数需要*100
         base[i] = base[i - ] *  % mod;
     cin >> l >> r >> s;
     cout << (solve(r, s) - solve(l - , s) + mod) % mod << endl;
     return ;
 }