2. Linear Regression with One Variable
Speaker:Andrew Ng
这一次主要讲解的是单变量的线性回归问题。
1.Model Representation
先来一个现实生活中的例子,这里的例子是房子尺寸和房价的模型关系表达。
通过学习Linear Regression可以进行预测某一size的房子prices是多少。

Regression问题属于Supervised Learning监督学习问题,预测连续值,Classification分类是预测离散值,上一个Introduction已经介绍过。

在上一张图的坐标点就是这里的训练集合。这里我们定义m是训练数据的数量或组数,x是输入变量或特征feature,y是输出变量target。) 代表一组训练数据,例如
代表一组训练数据,例如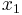 = 2104,
= 2104, 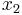 = 1416,
= 1416, 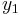 = 460.
= 460.

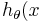=\theta_0+\theta_1x) 也可以简写成
也可以简写成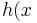) .那么我们如何来计算他的参数
.那么我们如何来计算他的参数 和
和 ?下面继续。
?下面继续。 和
和 的值。
的值。 ,
, so that
so that 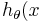) is close to
is close to 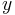 for out training examples
for out training examples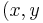) .
.









such that
2. Linear Regression with One Variable的更多相关文章
- Stanford机器学习---第二讲. 多变量线性回归 Linear Regression with multiple variable
原文:http://blog.csdn.net/abcjennifer/article/details/7700772 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...
- Stanford机器学习---第一讲. Linear Regression with one variable
原文:http://blog.csdn.net/abcjennifer/article/details/7691571 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...
- 机器学习笔记1——Linear Regression with One Variable
Linear Regression with One Variable Model Representation Recall that in *regression problems*, we ar ...
- Machine Learning 学习笔记2 - linear regression with one variable(单变量线性回归)
一.Model representation(模型表示) 1.1 训练集 由训练样例(training example)组成的集合就是训练集(training set), 如下图所示, 其中(x,y) ...
- Ng第二课:单变量线性回归(Linear Regression with One Variable)
二.单变量线性回归(Linear Regression with One Variable) 2.1 模型表示 2.2 代价函数 2.3 代价函数的直观理解 2.4 梯度下降 2.5 梯度下 ...
- 【cs229-Lecture2】Linear Regression with One Variable (Week 1)(含测试数据和源码)
从Ⅱ到Ⅳ都在讲的是线性回归,其中第Ⅱ章讲得是简单线性回归(simple linear regression, SLR)(单变量),第Ⅲ章讲的是线代基础,第Ⅳ章讲的是多元回归(大于一个自变量). 本文的 ...
- MachineLearning ---- lesson 2 Linear Regression with One Variable
Linear Regression with One Variable model Representation 以上篇博文中的房价预测为例,从图中依次来看,m表示训练集的大小,此处即房价样本数量:x ...
- 斯坦福第二课:单变量线性回归(Linear Regression with One Variable)
二.单变量线性回归(Linear Regression with One Variable) 2.1 模型表示 2.2 代价函数 2.3 代价函数的直观理解 I 2.4 代价函数的直观理解 I ...
- 机器学习 (一) 单变量线性回归 Linear Regression with One Variable
文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang的个人笔 ...
- Lecture0 -- Introduction&&Linear Regression with One Variable
Introduction What is machine learning? Tom Mitchell provides a more modern definition: "A compu ...
随机推荐
- apiAutoTest: 接口自动化测试的数据清洗(备份/恢复)处理方案
接口自动化测试之数据清洗/隔离/备份/恢复 在得到QQ:1301559180 得代码贡献之后,想到了通过ssh连接上服务器,然后进行数据库备份,数据库恢复, 主要使用了 paramiko库 最终效果 ...
- 攻防世界—pwn—level2
题目分析 题目提示 下载文件后首先使用checksec检查文件保护机制 使用ida打开,查看伪代码 搜索字符串发现/bash/sh 信息收集 偏移量 system的地址 /bin/sh的地址 编写脚本 ...
- 开发进阶:Dotnet Core多路径异步终止
今天用一个简单例子说说异步的多路径终止.我尽可能写得容易理解吧,但今天的内容需要有一定的编程能力. 今天这个话题,来自于最近对gRPC的一些技术研究. 话题本身跟gRPC没有太大关系.应用中,我用 ...
- Centos7 添加用户及设置权限
一.添加用户 1.登录root 用户 [gau@localhost /]$ su Password: # 输入密码 [root@localhost /]# 2.添加用户 [root@localhost ...
- 从ReentrantLock源码入手看锁的实现
写这篇确实挺伤脑筋的,是按部就班一行一行读,但是我想这么写估计很多没有接触过的可能就劝退了,很容易出现的一种现象就是看了后面忘了前面,而且很容易看了一行代码就一层层往下钻,这样不仅容易打击看源码的积极 ...
- 同步与异步 Python 有何不同?
你是否听到人们说过,异步 Python 代码比"普通(或同步)Python 代码更快?果真是那样吗? 1 "同步"和"异步"是什么意思? Web 应用 ...
- Java语法糖详解
语法糖 语法糖(Syntactic Sugar),也称糖衣语法,是由英国计算机学家 Peter.J.Landin 发明的一个术语,指在计算机语言中添加的某种语法,这种语法对语言的功能并没有影响,但是更 ...
- 一篇文章带你初步了解—CSS特指度
CSS特指度 说明 这篇博客在在两台电脑上分别完成的,故而有些截图是Firefox,有些是Chrome,有些改动了浏览器的用户样式表,有些没改,但不会影响阅读,特此说明,勿怪. CSS选择器 单个CS ...
- 下面给出一个child-parent的表格,要求挖掘其中的父子辈关系,给出祖孙辈关系的表格。
package org.apache.hadoop.examples; import java.util.HashMap; import java.io.IOException; import jav ...
- 一站式入口服务|爱奇艺微服务平台 API 网关实战 原创 弹性计算团队 爱奇艺技术产品团队
一站式入口服务|爱奇艺微服务平台 API 网关实战 原创 弹性计算团队 爱奇艺技术产品团队
