BZOJ1854 连续攻击游戏 题解

题目

lxhgww最近迷上了一款游戏，在游戏里，他拥有很多的装备，每种装备都有2个属性，这些属性的值用[1,10000]之间的数表示。当他使用某种装备时，他只能使用该装备的某一个属性。并且每种装备最多只能使用一次。 游戏进行到最后，lxhgww遇到了终极boss，这个终极boss很奇怪，攻击他的装备所使用的属性值必须从1开始连续递增地攻击，才能对boss产生伤害。也就是说一开始的时候，lxhgww只能使用某个属性值为1的装备攻击boss，然后只能使用某个属性值为2的装备攻击boss，然后只能使用某个属性值为3的装备攻击boss……以此类推。 现在lxhgww想知道他最多能连续攻击boss多少次？

输入格式

输入的第一行是一个整数N，表示lxhgww拥有N种装备 接下来N行，是对这N种装备的描述，每行2个数字，表示第i种装备的2个属性值

输出格式

输出一行，包括1个数字，表示lxhgww最多能连续攻击的次数。

输入样例

3
1 2
3 2
4 5

输出样例

2

题解

BZOJ日常挂...

洛谷AC:

先说操作:

把武器的两个属性当作节点, 如果父亲不相等, 用并查集合并起来, 数值大的节点做父节点, 数值小的标记, 如果数值相等, 标记父亲

从\(1\)开始, 扫描每个节点(无论是否出现过), 如果\(i\)没有被标记, 就输出\(i-1\)

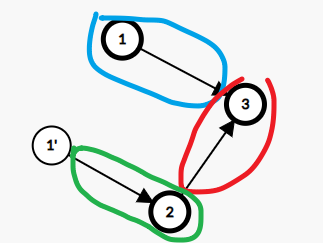
对应样例的图:

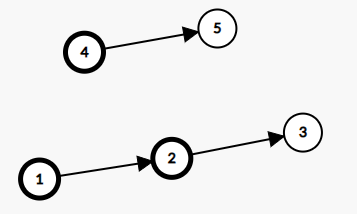
加粗边缘的节点是已标记的

从\(1\)扫描到\(3\), 未标记, 输出\(2\)

为什么要输出\(i-1\)呢? 很简单

红线圈住的部分是每个武器

因为每个武器只能使用一个属性, 所以最开始\(1-2\), 只标记了\(1\), 而后来\(2\)之所以也被标记, 是因为又出现了一个属性里含\(2\)的武器, 对于这个新武器, 不使用值为\(3\)的属性, 使用值为\(2\)的属性是完全没问题的, 不需要考虑之前的武器使用了什么.

由于从小到大依次使用属性, 所以被标记的是小的

这个\(4-5\)有什么作用? 如果又出现一个\(3-4\)武器, 那么图就会变成这样:

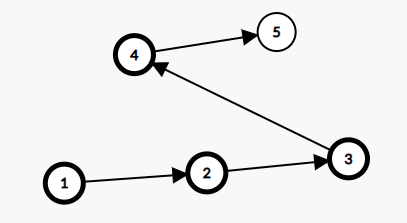
所以保存其它的属性是为了以后的可能存在的更优解

---

但是, 题中还要求使用的属性必须每次递增1, 如果武器的属性不是相差\(1\)呢?

比如这样的图:

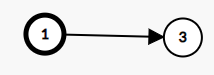
输出为\(1\), 是正确的, 原因就是从\(1\)遍历到\(2\)的时候, \(2\)虽然没有出现过, 但也要遍历, 也要检查是否被标记, 当然没有被标记, 所以直接输出\(2-1=1\)了, 遍历过程中还发现这条路断了(\(1-2-3\)中缺失\(2\)), 就输出能走到的最大节点\(1\)

如果还有一个武器是\(2-3\)的话, 图就会变成这样:

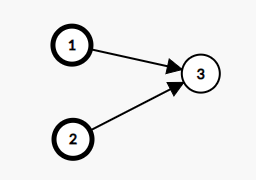
输出显然是\(2\)

别忘了, 当武器的两个属性父亲相等的时候, 直接标记父节点, 假设又出现了一个\(1-2\)武器, \(2\)和\(3\)的父亲是\(3\), 相等, 那么图变成这样:

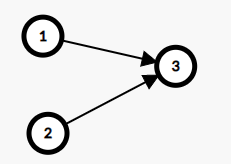
\(3\)节点也被标记了, 输出是\(3\), 这个怎么理解呢?

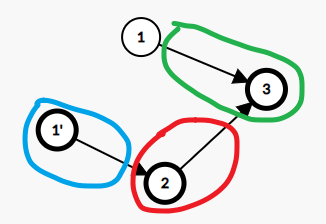
原本\(1-3\)武器不再使用属性值\(1\),转而使用\(3\), 因为新加入的武器含属性值\(1\), 可以代替它执行\(1\)的职责

同理, 这个也可以看作\(2-3\)武器不再使用属性值\(2\),转而使用\(3\), 因为新加入的武器含属性值\(2\), 可以代替它执行\(2\)的职责:

代码

#include <cstdio>
#include <iostream>
int n, fa[1000005],x,y,p,q;
bool vis[1000005];
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
bool join(int x, int y) {
    if (x < y) std::swap(x, y);
    vis[y] = 1, fa[y] = x;
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n + 1; i++) fa[i] = i;
    for (int i = 1; i <= n; i++) {
        scanf("%d%d", &x, &y);
        if((p = find(x)) == (q = find(y))) vis[p] = 1;
        else join(p, q);
    }
    for (int i = 1; i <= n + 1; i++)
        if (!vis[i]) {
            printf("%d", i - 1);
            break;
        }
    return 0;
}