全排列（dfs）

无重复元素的全排列

输入n（<=11），按从小到大输出数字1 到n 个的全部排列。
样例：
输入：
3
输出：
1:1 2 3
2:1 3 2
3:2 1 3
4:2 3 1
5:3 1 2
6:3 2 1

全排列可以用STL来写，但为了强化dfs，就用 dfs 吧。

看了某一个pdf，我对搜索有了一个更深的认识。就是关于如何去dfs，我认为可以从这两方面想：一是能否转化为图的问题，二是能否画出搜索树。只要这两种有一个能想出来，那么dfs就一定能写出来。

而能否转化成图的这类题目，一般元素都是固定的，也就是说，图上的结点就固定了。就比如说这个全排列，元素就是1到n固定不变，那么这1到n个数就可以转化成图上的n个结点，其中每两个点之间都连一条边，然后不重复的遍历所有的点就行了。

既然这个图都能想出来，那搜索树就一定能画出来了，这里就不讲了。

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 #define rep(i, a, n) for(int i = a; i <= n; ++i)
 #define per(i, n, a) for(int i = n; i >= a; --i)
 typedef long long ll;
 int n, ans[], tot = ;
 int vis[];
 void print(int x)
 {
     printf("%d:", x);
     rep(i, , n) printf("%d ", ans[i]); printf("\n");
 }
 void solve(int x, int step)
 {
     ans[step] = x; vis[x]= ;
     if(step == n) print(++tot);
     rep(i, , n)
     {
         if(!vis[i])
         {
             solve(i, step + );
             vis[i] = ;
         }
     }
 }
 
 int main()
 {
 //    freopen("p1.in", "r", stdin);
 //    freopen("p1.out", "w", stdout);
     scanf("%d", &n);
     rep(i, , n)　　　　//从每一个结点出发，遍历方式都不同
     {
         memset(vis, , sizeof(vis));
         solve(i, );
     }
     return ;
 }

有重复元素的全排列

输入n（<=10）个小些字母（可能重复），按从小到大输出输出n 个字符的全部排列。
样例：
输入：
abaab
输出：
1:aaabb
2:aabab
3:aabba
4:abaab
5:ababa
6:abbaa
7:baaab
8:baaba
9:babaa
10:bbaaa

这道题跟全排列相比，元素可以重复。如果全排列方式建图的话，比如下图

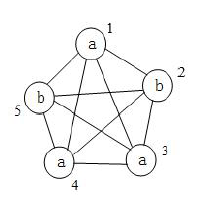
会发现从1,3,4结点出发点的边，遍历的结果是一样的，从2和5出发也是一样。所以对于同一个字母，我们只希望从该点出发一次。

用vis数组标记共字母种类n，然后遍历n次

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 #define rep(i, a, n) for(int i = a; i <= n; ++i)
 #define per(i, n, a) for(int i = n; i >= a; --i)
 typedef long long ll;
 int tot = , len;
 char a[], ans[];
 int vis[];
 void print(int tot)
 {
     printf("%d:%s\n", tot, ans + );
 }
 void dfs(int x)
 {
     if(x == len + ) print(++tot);
     rep(i, 'a', 'z')
     {
         if(vis[i])        //存在这个点
         {
             ans[x] = i;
             vis[i]--;    //表示这个点已经走过
             dfs(x + );
             vis[i]++;
         }
     }
 }
 int main()
 {
 //    freopen("p3.in", "r", stdin);
 //    freopen("p3.out", "w", stdout);
     scanf("%s", a);
     len = strlen(a);
     sort(a, a + len);
     rep(i, , len - ) vis[a[i]]++;
     dfs();
     return ;
 }