独立成分分析（Independent component analysis, ICA）

作者：桂。

时间：2017-05-22 12:12:43

链接：http://www.cnblogs.com/xingshansi/p/6884273.html

---

前言

今天群里冒出这样一个问题：群里谁有INFORMAX语音分离源程序？看到要程序的就头大，这是一个盲源分离问题，之前没有推导过，借此过一遍思路。

一、问题描述

　　经典的鸡尾酒宴会问题（cocktail party problem）。假设在party中有n个人，他们可以同时说话，我们也在房间中一些角落里共放置了n个声音接收器（Microphone）用来记录声音。宴会过后，我们从n个麦克风中得到了一组数据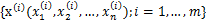，i表示采样的时间顺序，也就是说共得到了m组采样，每一组采样都是n维的。我们的目标是单单从这m组采样数据中分辨出每个人说话的信号。

将第二个问题细化一下，有n个信号源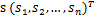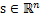，，每一维都是一个人的声音信号，每个人发出的声音信号独立。A是一个未知的混合矩阵（mixing matrix），用来组合叠加信号s，那么

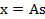
x的意义在上文解释过，这里的x不是一个向量，是一个矩阵。其中每个列向量是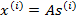， ，表示成图就是：

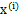的每个分量都由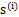的分量线性表示。A和s都是未知的，x是已知的，我们要想办法根据x来推出s。这个过程也称作为盲信号分离。

令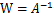，那么

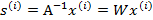
将W表示成

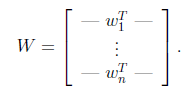
其中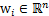，其实就是将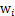写成行向量形式。那么得到：

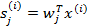
ICA的主要任务是估计解混矩阵W。

二、理论求解(不感兴趣可跳过)

　　A-理论基础

标准ICA理论有几个支撑点：

1）各源信号统计独立；

2）至多有一个源信号服从Gauss分布

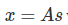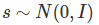对于，并假设，则有：

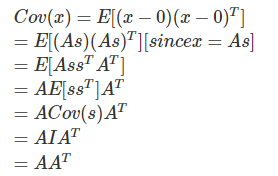
另一方面，对于任意正交矩阵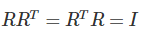：，令：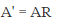

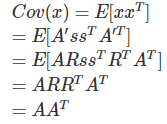
可见混合矩阵无法有效估计。

3）混合矩阵为方阵

　　B-理论求解

1-中心极限定理：

中心极限定理表明：对于混合信号，其概率密度比任何一个源信号的概率分布都接近高斯分布;反过来，最大化信号的非高斯性与最大化信号的统计独立性是一致的，只是ICA的基本原理。

2-非高斯性度量

a)利用统计量

峭度（kurtosis）

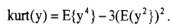
峭度基本性质：

b)利用信息论知识

熵的定义：

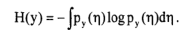
负熵：

给出基于KL散度的定义：

互信息:

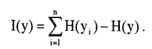
考虑负熵的定义，上式重写为：

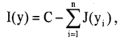
该式表明：最小化互信息等价于最大化负熵。

对于负熵，有时为了简化常用近似的方法：

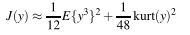
上面的逼近通常不够理想，改进版的近似：

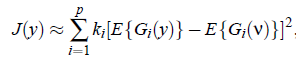
其中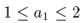，且：

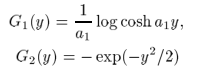
c)利用概率估计

利用MLE准则进行参数估计。

三、算法实现

给出利用概率估计的算法原理，准则函数（取对数）：

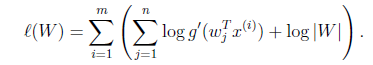
其中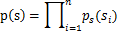：，从而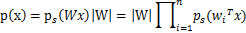。这里的g表示概率密度，可以用sigmoid函数，也可以用tan函数等等，以sigmoid函数为例：

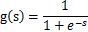
由于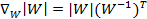：，利用梯度下降法求解。给出梯度的计算公式：

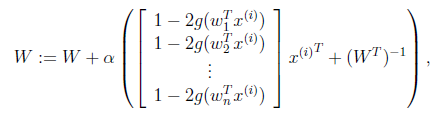给出主要code实现：

for iter=1:length(anneal)
    iter
   % Randomly interate through the samples running stochastic gradient descent
   rowIndices = randperm(m);
   for i = 1:length(rowIndices)
      rowIndex = rowIndices(i);
      % Perform the ICA stochastic gradient descent update
      W = W + anneal(iter) * ((ones(n,1)-2*ones(n,1)./(ones(n,1)+exp(-W*mix(rowIndex,:)')))*mix(rowIndex,:) + (W')^-1);
   end
end;

四、其他

　　A-ICA的不确定性

1-分离信号幅度与初始相位的不确定性

信源信号S和混合矩阵A：

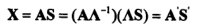
可以看出，对于实数信号产生幅度不确定性，对于复数信号，产生幅度与相位的不确定性。

幅度的不确定性可以采用假设信号单位方差的方法修正。

2-分离信号的次序不确定性

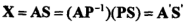
P是任意置换矩阵，这就造成了分离信号次序的不确定性。

　　B-ICA中的预处理

1-中心化

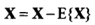
ICA算法中，均值为零可以使得很多相乘项为零，简化算法复杂性。

2-白化处理

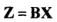
B为白化矩阵。白化操作之前有介绍，白化处理已经包含了中心化。ICA中的白化通常指满秩的白化。

白化的本质就是旋转+方差单位化。白化操作是去除信号的相关性，以基于信息论的ICA为例，各个概率密度独立是理论假设的基本前提。

参考

• 
• http://www.cnblogs.com/jerrylead/archive/2011/04/19/2021071.html