【HNOI2014】米特运输

题面

题解

首先我们需要看懂题目

然后我们需要发现一个结论

只要有一个节点的权值确定，那么整棵树的权值就确定了

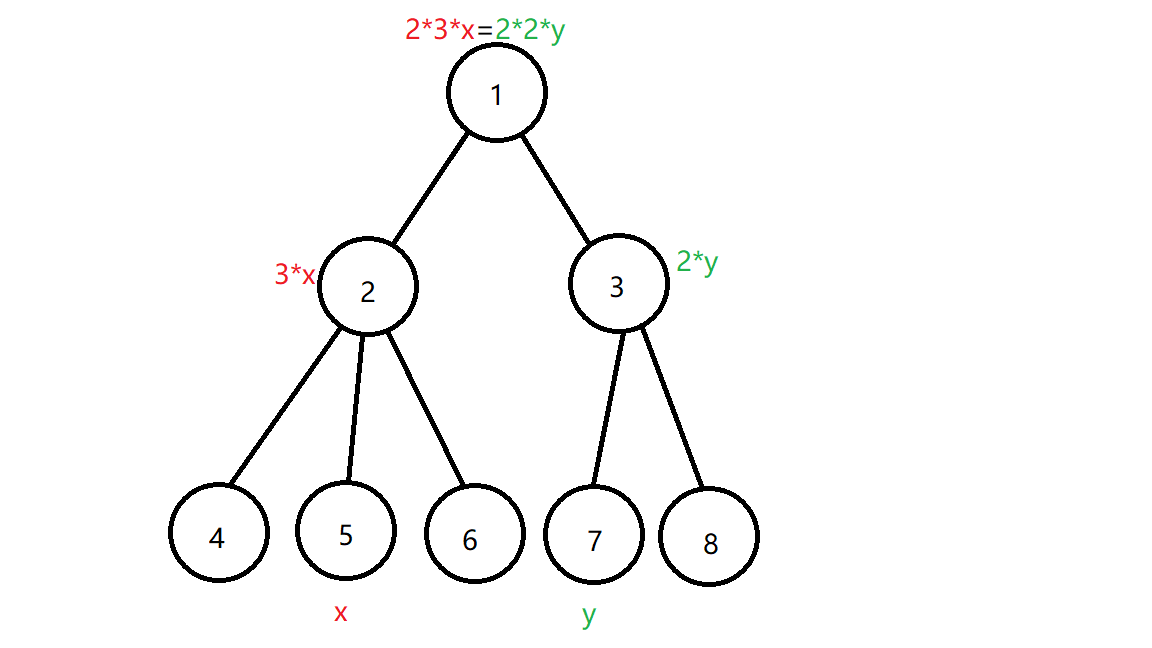
就像这样：（图片来源于网络，侵删）

然后我们根据这张图片，可以设\(f[i] = a[i] \cdot \prod_f \mathrm{son}[f]\)

其中\(f\)是\(i\)的祖先，\(\mathrm{son}[f]\)表示\(f\)的子节点的个数，\(a[i]\)表示\(i\)的权值

于是我们可以用显然法证明当\(f[i] = f[j]\)时，\(i\)和\(j\)的权值肯定在一种方案中都不用修改

于是算出最多有多少点的\(f\)值相等

然后你愉快地打了上去，oho了

\(f[]\)会爆long long，于是考虑取对数就可以了

普及公式：\(\log_c a + \log_c b = \log_c (ab)\)

代码

#include<cstdio>
#include<cstring>
#include<cmath>
#include<cctype>
#include<algorithm>
#define RG register
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define clear(x, y) memset(x, y, sizeof(x))

inline int read()
{
	int data = 0, w = 1; char ch = getchar();
	while(ch != '-' && (!isdigit(ch))) ch = getchar();
	if(ch == '-') w = -1, ch = getchar();
	while(isdigit(ch)) data = data * 10 + (ch ^ 48), ch = getchar();
	return data * w;
}

const double eps(1e-8);
const int maxn(500010);
struct edge { int next, to; } e[maxn];
int head[maxn], e_num, n, a[maxn], deg[maxn];
double f[maxn];

inline void add_edge(int from, int to)
{
	e[++e_num] = (edge) {head[from], to};
	head[from] = e_num;
}

void dfs(int x, double s)
{
	f[x] = s + log(a[x]);
	for(RG int i = head[x]; i; i = e[i].next)
		dfs(e[i].to, s + log(deg[x]));
}

int main()
{
	n = read();
	for(RG int i = 1; i <= n; i++) a[i] = read();
	for(RG int i = 1, a, b; i < n; i++)
		a = read(), b = read(), ++deg[a], add_edge(a, b);
	dfs(1, 0); std::sort(f + 1, f + n + 1); int ans = 1;
	for(RG int i = 2, cnt = 1; i <= n; i++)
	{
		if(f[i] - f[i - 1] <= eps) ans = std::max(ans, ++cnt);
		else cnt = 1;
	}
	printf("%d\n", n - ans);
	return 0;
}