【IUML】支持向量机SVM[续]
支持向量机基本上是最好的有监督学习算法了。看很多正统的讲法都是从VC 维理论和结构风险最小原理出发,然后引出SVM什么的,还有些资料上来就讲分类超平面什么的。我们logistic回归出发,引出了SVM,既揭示了模型间的联系,也让人觉得过渡更自然。
logistic回归
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。形式化表示就是假设函数
其中x是n维特征向量,函数g就是logistic函数。
图像如下所示:
可以看到,将无穷映射到了(0,1)。而假设函数就是特征属于y=1的概率。
当我们要判别一个新来的特征属于哪个类时,只需求
再审视一下






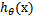 =1,反之
=1,反之




图形化表示如下:

中间那条线是
形式化表示
我们这次使用的结果标签是y=-1,y=1,替换在logistic回归中使用的y=0和y=1。同时将





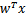 )。这样,我们让
)。这样,我们让

上一节提到过我们只需考虑
函数间隔(functional margin)和几何间隔(geometric margin)
给定一个训练样本
可想而知,当







刚刚我们定义的函数间隔是针对某一个样本的,现在我们定义全局样本上的函数间隔
说白了就是在训练样本上分类正例和负例确信度最小那个函数间隔。接下来定义几何间隔,先看图
假设我们有了B点所在的





进一步得到
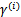 实际上就是点到平面距离。
实际上就是点到平面距离。
再换种更加优雅的写法:
当


最优间隔分类器(optimal margin classifier)
回想前面我们提到我们的目标是寻找一个超平面,使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面,我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。形象的说,我们将上面的图看作是一张纸,我们要找一条折线,按照这条折线折叠后,离折线最近的点的间距比其他折线都要大。形式化表示为:
这里用

到此,我们已经将模型定义出来了。如果求得了w和b,那么来一个特征x,我们就能够分类了,称为最优间隔分类器。接下的问题就是如何求解w和b的问题了。
由于

这时候其实我们求的最大值仍然是几何间隔,只不过此时的w不受
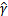 做一些限制,以保证我们解是唯一的。这里为了简便我们取
做一些限制,以保证我们解是唯一的。这里为了简便我们取



只有线性约束了,而且是个典型的二次规划问题(目标函数是自变量的二次函数)。代入优化软件可解。到这里发现,画好分类超平面,在图上标示出间隔那么直观,但每一步推导有理有据,依靠思路的流畅性来推导出目标函数和约束。
======================================================== 转载请注明出处:http://blog.csdn.net/utimes/article/details/9259301 ========================================================【IUML】支持向量机SVM[续]的更多相关文章
- 【IUML】支持向量机SVM
从1995年Vapnik等人提出一种机器学习的新方法支持向量机(SVM)之后,支持向量机成为继人工神经网络之后又一研究热点,国内外研究都很多.支持向量机方法是建立在统计学习理论的VC维理论和结构风险最 ...
- 机器学习——支持向量机SVM
前言 学习本章节前需要先学习: <机器学习--最优化问题:拉格朗日乘子法.KKT条件以及对偶问题> <机器学习--感知机> 1 摘要: 支持向量机(SVM)是一种二类分类模型, ...
- 机器学习:Python中如何使用支持向量机(SVM)算法
(简单介绍一下支持向量机,详细介绍尤其是算法过程可以查阅其他资) 在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别.分类(异 ...
- 以图像分割为例浅谈支持向量机(SVM)
1. 什么是支持向量机? 在机器学习中,分类问题是一种非常常见也非常重要的问题.常见的分类方法有决策树.聚类方法.贝叶斯分类等等.举一个常见的分类的例子.如下图1所示,在平面直角坐标系中,有一些点 ...
- 机器学习算法 - 支持向量机SVM
在上两节中,我们讲解了机器学习的决策树和k-近邻算法,本节我们讲解另外一种分类算法:支持向量机SVM. SVM是迄今为止最好使用的分类器之一,它可以不加修改即可直接使用,从而得到低错误率的结果. [案 ...
- 机器学习之支持向量机—SVM原理代码实现
支持向量机—SVM原理代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9596898.html 1. 解决 ...
- 支持向量机SVM——专治线性不可分
SVM原理 线性可分与线性不可分 线性可分 线性不可分-------[无论用哪条直线都无法将女生情绪正确分类] SVM的核函数可以帮助我们: 假设‘开心’是轻飘飘的,“不开心”是沉重的 将三维视图还原 ...
- 一步步教你轻松学支持向量机SVM算法之案例篇2
一步步教你轻松学支持向量机SVM算法之案例篇2 (白宁超 2018年10月22日10:09:07) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
- 一步步教你轻松学支持向量机SVM算法之理论篇1
一步步教你轻松学支持向量机SVM算法之理论篇1 (白宁超 2018年10月22日10:03:35) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
随机推荐
- Ruby windows7安装配置(最新版本)
1.下载最新版本的rubyinstaller并安装http://rubyinstaller.org/downloads/ 如下图所示设置路径,我安装时将所有选项都打够了,免除了后面需要什么配置麻烦. ...
- 《Android源码设计模式》--原型模式
No1: 原型模式使用场景: 1)类初始化需要消耗非常多的资源,这个资源包括数据.硬件资源等,通过原型复制避免这些消耗 2)通过new产生一个对象需要非常繁琐的数据准备货访问权限,这是可以使用原型模式 ...
- CSUOJ 1341 String and Arrays
Description 有一个N*N的字符矩阵,从上到下依次记为第1行,第2行,--,第N行,从左至右依次记为第1列,第2列,--,第N列. 对于这个矩阵会进行一系列操作,但这些操作只有两类: ...
- 海康威视 - 萤石云开放平台 js 版
开放平台 https://open.ys7.com/mobile/download.html API http://open.ys7.com/doc/zh/uikit/uikit_javascript ...
- JavaQuery操作对象
1.jQuery操作的分类 <!DOCTYPE html> <html> <head lang="en"> <meta cha ...
- JQuery基础-DAY1
jQuery介绍 是一个轻量级的js框架/库,其宗旨是write less do more. jQuery对象 js的对象叫做dom对象 使用jQuery框架产生的对象是jQuery对象,是对dom对 ...
- [Agc002E]Candy Piles
[Agc002E]Candy Piles 题目大意 有\(n\)个数,两人轮流操作,可以做以下操作之一: 删掉一个最大的数 将所有数-1 最后取没的人输,问先手是否必胜? 试题分析 直接决策不知道选哪 ...
- 【set】【可持久化Trie】The 16th UESTC Programming Contest Preliminary K - Will the circle be broken
题意:You are given an array A of N non-negative integers and an integer M. Find the number of pair(i,j ...
- C# 传统的ToString
C# 传统的ToString DataRow dr=item; var str=dr["Name"]; str.ToString();//dr["Name"]= ...
- HashMap和Hashtable的区别--List,Set,Map等接口是否都继承自Map接口--Collection和Collections的区别
面试题: 1.HashMap和Hashtable的区别? HashMap:线程不安全,效率高,键和值都允许null值 Hashtable:线程安全,效率低,键和值都不允许null值 ArrayList ...















