Codeforces 15E Triangles 【组合计数】

Codeforces 15E Triangles

---

Last summer Peter was at his granny’s in the country, when a wolf attacked sheep in the nearby forest. Now he fears to walk through the forest, to walk round the forest, even to get out of the house. He explains this not by the fear of the wolf, but by a strange, in his opinion, pattern of the forest that has n levels, where n is an even number.

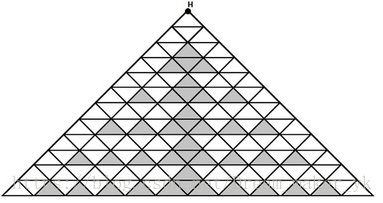
In the local council you were given an area map, where the granny’s house is marked by point H, parts of dense forest are marked grey (see the picture to understand better).

After a long time at home Peter decided to yield to his granny’s persuasions and step out for a breath of fresh air. Being prudent, Peter plans the route beforehand. The route, that Peter considers the most suitable, has the following characteristics:

it starts and ends in the same place — the granny’s house;

the route goes along the forest paths only (these are the segments marked black in the picture);

the route has positive length (to step out for a breath of fresh air Peter has to cover some distance anyway);

the route cannot cross itself;

there shouldn’t be any part of dense forest within the part marked out by this route;

You should find the amount of such suitable oriented routes modulo 1000000009.

The example of the area map for n = 12 is given in the picture. Since the map has a regular structure, you can construct it for other n by analogy using the example.

Input

The input data contain the only even integer n (2 ≤ n ≤ 106).

Output

Output the only number — the amount of Peter’s routes modulo 1000000009.

Examples

input

2

output

10

input

4

output

74

---

先大大的%yyf大神的blog 大神blog

讲的贼详细

好吧

这题看起来挺麻烦的

但是我们发现首先方向是可以直接乘2乘掉的，其次两边的情况是可以平方掉的

然后我们只需要考虑一遍的情况了

然后我们找一下规律发现

对于每个



这样的东东，每一层（两行）倒着的三角的个数和在这一行折返的方案数是可以找到规律的

tipi=tipi−1∗2+3" role="presentation">tipi=tipi−1∗2+3tipi=tipi−1∗2+3

然后累乘一下就好啦

#include<bits/stdc++.h>
using namespace std;
#define yyf 1000000009
int main(){
    long long ans=2,n,tip1=1,tip2=1;
    cin>>n;n/=2;
    if(n==1){cout<<10;return 0;}
    n--;
    while(n--){
        ans=(ans+tip2*4)%yyf;
        tip1=(tip1*2+3)%yyf;
        tip2=(tip2*tip1)%yyf;
    }
    ans=(ans*ans%yyf*2+2)%yyf;
    cout<<ans;
    return 0;
}