Android Matrix理论与应用详解

转：http://zensheno.blog.51cto.com/2712776/513652

Matrix学习——基础知识

以前在线性代数中学习了矩阵，对矩阵的基本运算有一些了解，前段时间在使用GDI+的时候再次学习如何使用矩阵来变化图像，看了之后在这里总结说明。

首先大家看看下面这个3 x 3的矩阵，这个矩阵被分割成4部分。为什么分割成4部分，在后面详细说明。

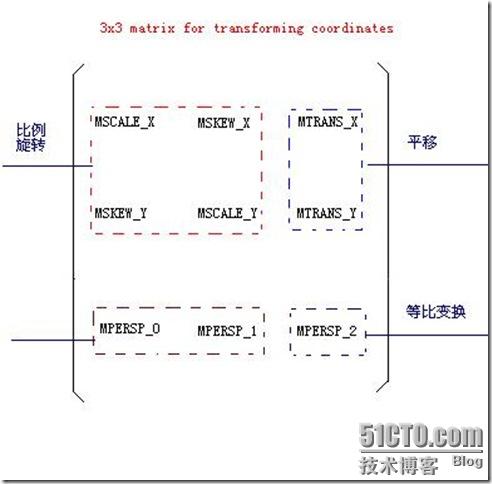
首先给大家举个简单的例子：现设点P0（x0， y0）进行平移后，移到P（x，y），其中x方向的平移量为△x，y方向的平移量为△y，那么，点P（x，y）的坐标为：

x = x0  + △x 
y = y0  + △y

采用矩阵表达上述如下： 

上述也类似与图像的平移，通过上述矩阵我们发现，只需要修改矩阵右上角的2个元素就可以了。

我们回头看上述矩阵的划分： 

为了验证上面的功能划分，我们举个具体的例子：现设点P0（x0 ，y0）进行平移后，移到P（x，y），其中x放大a倍，y放大b倍，

矩阵就是：，按照类似前面“平移”的方法就验证。

图像的旋转稍微复杂：现设点P0（x0， y0）旋转θ角后的对应点为P（x， y）。通过使用向量，我们得到如下：

x0 = r cosα 
y0 = r sinα

x = r cos(α+θ) = x0 cosθ - y0 sinθ 
y = r sin(α+θ) = x0 sinθ + y0 cosθ

于是我们得到矩阵：

如果图像围绕着某个点(a ，b)旋转呢？则先要将坐标平移到该点，再进行旋转，然后将旋转后的图像平移回到原来的坐标原点，在后面的篇幅中我们将详细介绍。

Matrix学习——如何使用Matrix

上一篇幅 Matrix学习——基础知识，从高等数学方面给大家介绍了Matrix，本篇幅我们就结合Android 中的android.graphics.Matrix来具体说明，还记得我们前面说的图像旋转的矩阵：

从最简单的旋转90度的是：

在android.graphics.Matrix中有对应旋转的函数： 
Matrix matrix = new Matrix(); 
matrix.setRotate(90); 
Test.Log(MAXTRIX_TAG,”setRotate(90):%s” , matrix.toString());

查看运行后的矩阵的值（通过Log输出）：

与上面的公式基本完全一样（android.graphics.Matrix采用的是浮点数，而我们采用的整数）。

有了上面的例子，相信大家就可以亲自尝试了。通过上面的例子我们也发现，我们也可以直接来初始化矩阵，比如说要旋转30度：

前面给大家介绍了这么多，下面我们开始介绍图像的镜像，分为2种：水平镜像、垂直镜像。先介绍如何实现垂直镜像，什么是垂直镜像就不详细说明。图像的垂直镜像变化也可以用矩阵变化的表示，设点P0（x0 ，y0 ）进行镜像后的对应点为P（x ，y ），图像的高度为fHeight，宽度为fWidth，原图像中的P0（x0 ，y0 ）经过垂直镜像后的坐标变为（x0 ，fHeight- y0）； 
x = x0 
y = fHeight – y0 
推导出相应的矩阵是：

final float f[] = {1.0F,0.0F,0.0F,0.0F,-1.0F,120.0F,0.0F,0.0F,1.0F}; 
Matrix matrix = new Matrix(); 
matrix.setValues(f);

按照上述方法运行后的结果： 

至于水平镜像采用类似的方法，大家可以自己去试试吧。

实际上，使用下面的方式也可以实现垂直镜像： 
Matrix matrix = new Matrix(); 
matrix.setScale (1.0，-1.0); 
matrix.postTraslate(0, fHeight);

这就是我们将在后面的篇幅中详细说明。

Matrix学习——图像的复合变化

Matrix学习——基础知识篇幅中，我们留下一个话题：如果图像围绕着某个点P(a，b)旋转，则先要将坐标系平移到该点，再进行旋转，然后将旋转后的图像平移回到原来的坐标原点。

我们需要3步：

1. 平移——将坐标系平移到点P(a，b)；

2. 旋转——以原点为中心旋转图像；

3. 平移——将旋转后的图像平移回到原来的坐标原点；

相比较前面说的图像的几何变化（基本的图像几何变化），这里需要平移——旋转——平移，这种需要多种图像的几何变化就叫做图像的复合变化。

设对给定的图像依次进行了基本变化F1、F2、F3…..、Fn，它们的变化矩阵分别为T1、T2、T3…..、Tn，图像复合变化的矩阵T可以表示为：T = TnTn-1…T1。

按照上面的原则，围绕着某个点(a，b)旋转θ的变化矩阵序列是：

按照上面的公式，我们列举一个简单的例子：围绕（100，100）旋转30度(sin 30 = 0.5 ，cos 30 = 0.866) 
float f[]= { 0.866F,  -0.5F, 63.4F,0.5F, 0.866F,-36.6F,0.0F,    0.0F,  1.0F }; 
matrix = new Matrix(); 
matrix.setValues(f); 
旋转后的图像如下：

Android为我们提供了更加简单的方法，如下： 
Matrix matrix = new Matrix(); 
matrix.setRotate(30，100，100); 
矩阵运行后的实际结果： 
 
与我们前面通过公式获取得到的矩阵完全一样。

在这里我们提供另外一种方法，也可以达到同样的效果： 
float a = 100.0F,b = 100.0F; 
matrix = new Matrix(); 
matrix.setTranslate(a,b); 
matrix.preRotate(30); 
matrix.preTranslate(-a,-b); 
将在后面的篇幅中为大家详细解析

通过类似的方法，我们还可以得到：相对点P(a，b)的比例[sx,sy]变化矩阵

Matrix学习——Preconcats or Postconcats?

从最基本的高等数学开始，Matrix的基本操作包括：+、*。Matrix的乘法不满足交换律，也就是说A*B ≠B*A。

还有2种常见的矩阵：

有了上面的基础，下面我们开始进入主题。由于矩阵不满足交换律，所以用矩阵B乘以矩阵A，需要考虑是左乘（B*A），还是右乘（A*B）。在Android的android.graphics.Matrix中为我们提供了类似的方法，也就是我们本篇幅要说明的Preconcats matrix 与 Postconcats  matrix。下面我们还是通过具体的例子还说明：

通过输出的信息，我们分析其运行过程如下：

看了上面的输出信息。我们得出结论：Preconcats matrix相当于右乘矩阵，Postconcats  matrix相当于左乘矩阵。

上一篇幅中，我们说到：

其晕死过程的详细分析就不在这里多说了。

Matrix学习——错切变换

什么是图像的错切变换（Shear transformation）？我们还是直接看图片错切变换后是的效果：

对图像的错切变换做个总结：

x = x0 + b*y0;

y = d*x0 + y0;

这里再次给大家介绍一个需要注意的地方：

通过以上，我们发现Matrix的setXXXX()函数，在调用时调用了一次reset()，这个在复合变换时需要注意。

Matrix学习——对称变换（反射）

什么是对称变换？具体的理论就不详细说明了，图像的镜像就是对称变换中的一种。

利用上面的总结做个具体的例子，产生与直线y= – x对称的反射图形，代码片段如下：

当前矩阵输出是：

图像变换的效果如下：

 

附：三角函数公式

两角和公式

sin(a+b)=sinacosb+cosasinb

sin(a-b)=sinacosb-sinbcosa 

cos(a+b)=cosacosb-sinasinb

cos(a-b)=cosacosb+sinasinb

tan(a+b)=(tana+tanb)/(1-tanatanb)

tan(a-b)=(tana-tanb)/(1+tanatanb)

cot(a+b)=(cotacotb-1)/(cotb+cota) 

cot(a-b)=(cotacotb+1)/(cotb-cota)

倍角公式

tan2a=2tana/[1-(tana)^2]

cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^2

sin2a=2sina*cosa

半角公式

sin(a/2)=√((1-cosa)/2) sin(a/2)=-√((1-cosa)/2)

cos(a/2)=√((1+cosa)/2) cos(a/2)=-√((1+cosa)/2)

tan(a/2)=√((1-cosa)/((1+cosa)) tan(a/2)=-√((1-cosa)/((1+cosa))

cot(a/2)=√((1+cosa)/((1-cosa)) cot(a/2)=-√((1+cosa)/((1-cosa)) 

tan(a/2)=(1-cosa)/sina=sina/(1+cosa)

和差化积

2sinacosb=sin(a+b)+sin(a-b)

2cosasinb=sin(a+b)-sin(a-b) )

2cosacosb=cos(a+b)-sin(a-b)

-2sinasinb=cos(a+b)-cos(a-b)

sina+sinb=2sin((a+b)/2)cos((a-b)/2

cosa+cosb=2cos((a+b)/2)sin((a-b)/2)

tana+tanb=sin(a+b)/cosacosb

积化和差公式

sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]

cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]

sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]

诱导公式

sin(-a)=-sin(a)

cos(-a)=cos(a)

sin(pi/2-a)=cos(a)

cos(pi/2-a)=sin(a)

sin(pi/2+a)=cos(a)

cos(pi/2+a)=-sin(a)

sin(pi-a)=sin(a)

cos(pi-a)=-cos(a)

sin(pi+a)=-sin(a)

cos(pi+a)=-cos(a)

tga=tana=sina/cosa

万能公式

sin(a)= (2tan(a/2))/(1+tan^2(a/2))

cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))

tan(a)= (2tan(a/2))/(1-tan^2(a/2))

其它公式

a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中，tan(c)=b/a]

a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中，tan(c)=a/b]

1+sin(a)=(sin(a/2)+cos(a/2))^2

1-sin(a)=(sin(a/2)-cos(a/2))^2

其他非重点三角函数

csc(a)=1/sin(a)

sec(a)=1/cos(a)

双曲函数

sinh(a)=(e^a-e^(-a))/2

cosh(a)=(e^a+e^(-a))/2

tgh(a)=sinh(a)/cosh(a)