正规式与正规集，DFA与NFA

词法分析器的设计

词法分析器的功能：输入源程序、输出单词符号

词法分析器的设计：给出程序设计语言的单词规范——单词表， 对照单词表设计识别该语言所有单词的状态转换图， 根据状态转换图编写词法分析程序

字母表：一个有穷字符集，记为∑

字母表中每个元素称为字符

∑上的字(也叫字符串) 是指由∑中的字符所构成的一个有穷序列

不包含任何字符的序列称为空字，记为ε

用∑*表示∑上的所有字的全体，包含空字ε

例如: 设 ∑={a， b}，则，∑*={ε,a,b,aa,ab,ba,bb,aaa,...}

∑ * 的子集U和V的连接（积）定义为UV＝{ αβ | α∈U & β∈V }

V自身的 n次积记为V n =V V…V

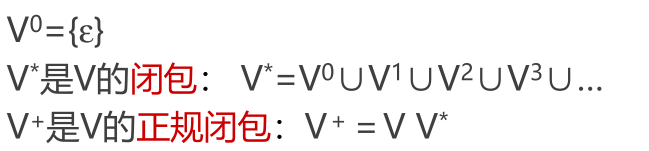
正规式和正规集

程序设计语言的单词符号都是一些特殊的字符串，用正规集和正规表达式（简称正规式）来描述

正规集可以用正规式表示，正规式是表示正规集一种方法， 一个字集合是正规集当且仅当它能用正规式表示

正规式和正规集的递归定义

对给定的字母表Σ，ε 和∅都是Σ上的正规式，它们所表示的正规集为{ε}和∅;

任何a∈Σ ，a是Σ上的正规式，它所表示的正规集为{a} ;

ε是什么？字，正规式

∅是什么？集合，正规式

a (a ∈Σ)是什么？字符，字，正规式

假定e 1 和e 2 都是Σ上的正规式，它们所表示的正规集为L(e 1 )和L(e 2 )，则(e 1 |e 2 )为正规式，它所表示的正规集为L(e 1 )∪L(e 2 )，(e 1 .e 2 )为正规式，它所表示的正规集为L(e 1 )L(e 2 )，(e 1 ) * 为正规式，它所表示的正规集为(L(e 1 )) *，仅由有限次使用上述三步骤而定义的表达式才是Σ上的正规式，仅由这些正规式表示的字集才是Σ上的正规集。

正规式的等价性

若两个正规式所表示的正规集相同，则称这两个正规式等价。如

正规式的性质

确定有限自动机

对状态图进行形式化定义

DFA表示为状态转换图，假定DFA M含有m个状态和n个输入字符，对应的状态转换图含有m个状态结点，每个结点顶多含有n条箭弧射出，且每条箭弧用Σ上的不同的输入字符来作标记

对于Σ*中的任何字α，若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于α，则称α为DFA M所识别(接收)，DFA M所识别的字的全体记为L(M)

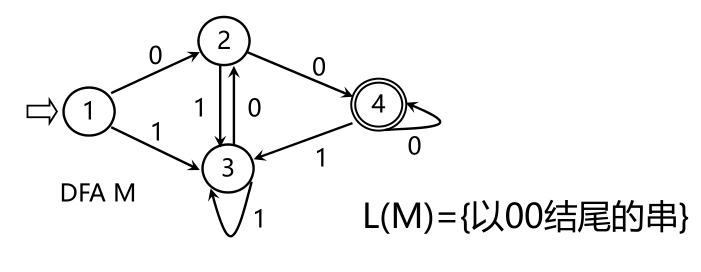
L(M)={含aa或bb的字}

非确定有限自动机

从状态图看NFA 和DFA的区别，NFA可以有多个初态，弧上的标记可以是Σ * 中的一个字(甚至可以是一个正规式)，而不一定是单个字符，同一个字可能出现在同状态射出的多条弧上

DFA是NFA的特例

对于Σ*中的任何字α，若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记字连接成的字等于α(忽略那些标记为ε的弧)，则称α为NFA M所识别(接收)，NFA M所识别的字的全体记为L(M)

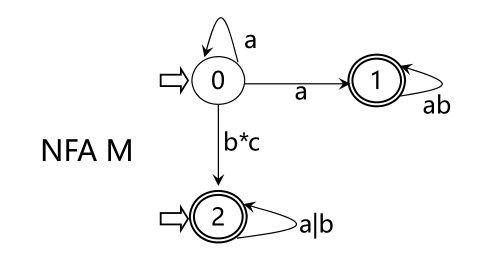
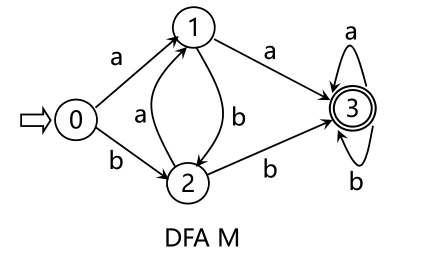
L(M 1 )={含aa或bb的字}

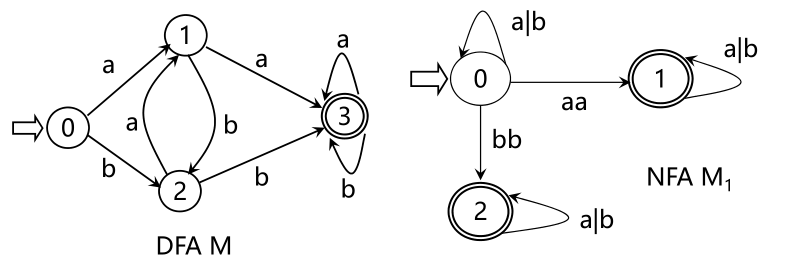
L(M 2 )={a m b n | m，n≥1}

DFA和NFA

定义：对于任何两个有限自动机M和M’，如果L(M)=L(M’)，则称M与M’等价，自动机理论中一个重要的结论：判定两个自动机等价性的算法是存在的，对于每个NFA M存在一个DFA M’，使得L(M)=L(M’)，DFA与NFA识别能力相同!