强连通分量——tarjan算法

概念：

有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量。

注：强联通分量仅仅是对有向图来说。

代码模板：

void tarjan(int x)
{
    cnt++;
    dfn[x] = low[x] =cnt;
    q.push(x);
    insta[x] =true;
    for(int i=head[x];i;i=edge[i].next )
    {
        int u =edge[i].to;
        if(!dfn[u])
        {
            tarjan(u);
            low[x] = min(low[x],low[u]);
        }else if(insta[u])
        {
            low[x] = min(low[x],dfn[u]);
        }
    }
    int k;
    if(low[x] == dfn[x])
    {
        num++;
        do{
            k =q.top();
            q.pop();
            insta[k] = false;
            id[k] = num;
        }while(k!=x);
    }
}

算法理解：

tarjan算法是一种基于DFS的算法，并且运用了数据结构栈。

此算法需要两个关键的数组：low[ ] 和 dfn[ ].

在我的理解看来：dfn[ ]数组是用来储存时间戳的，及何时访问到此节点。因此在每次对一个点进行DFS后，自己就形成了一个独一无二的时间戳，且永远不会改变。所以常一句dfn的值来判断是否需要进一步的深搜。

low[ ]数组用来储存与此节点相联通的节点的最小下标。因此low[ ]值相等的点在同一个强联通分量。

首先这个图不一定是一个连通图，所以跑Tarjan时要枚举每个点，若dfn[ ] == 0，进行深搜。进入深搜后，判断此点邻接点，如果邻接点的dfn[ ]为0，证明还没有访问过，就对此邻接点进行深搜，若dfn[ ]不为零，则判断此邻接点是否在栈中，若已经在栈中，则此时证明已经构成了环，则更新low[ ],与邻接点的时间戳进行比较，取最小值，例如下面这种情况：

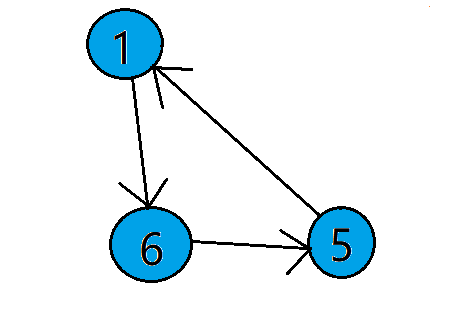
当对点5进行邻边搜索的时候，仅仅发现了点1，并且点1此时在栈中，这样，就构成了一个环。

在不断的深搜的过程中如果没有路可走了（已经没有出边了），那么就进行回溯，回溯时不断比较low[ ]， 取最小的low[ ]值。

如果dfn[x]==low[x],则此时x可以看作是强联通分量的根，就对栈进行弹出操作，直到x被弹出。

手动模拟一下过程：

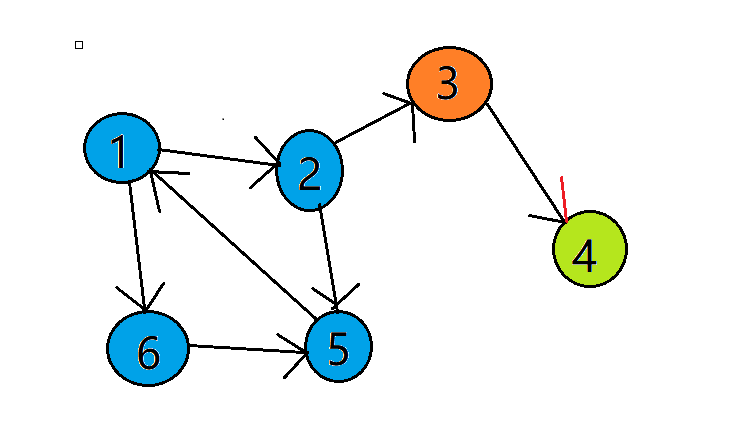
从1进入：dfn[1] =low[1] =++cnt = 1

入栈1: 1

从1进入2：dfn[2] = low[2] = ++cnt =2

入栈2: 12

从2进入3： dfn[3]=low[3] =++cnt =3;

入栈3: 123

从3进入4： dfn[4] = low[4] = ++cnt =4;

入栈4:1234；

4无出度，之后判断dfn[4] == low[4]；

4及4之前的点全部弹出

并且id[4] = ++num=1;

栈：123

并回溯到3

对low[3] = min(low[4],low[3])=3;

之后判断low[3] == dfn[3] =3;3及3以后的点弹出

id[3] = ++num=2;

栈：12；

继续回溯到2，对low[2] = min(low[2],low[3])=2;

从2 进入到5，dfn[5]=low[5] = ++cnt =5;

入栈5:125

从5进入1，由于1已经在栈中，则更新low[5] =min(low[5],dfn[1]) =1;

回溯到2，更新low[2 ] =min(low[2],low[5]) =1;

回溯到1，更新low[1] =min(low[1],low[2])=low[1] =1;

从1进入6，dfn[6] =low[6] = 6;

入栈6:1256

由于临点5已经在栈中，更新low[6] = min(low[6],low[5]) = 1;

回溯到1，由于low[1] ==dfn[1],则弹出1及一以上的点：
id[1] = id[2] =id[5] = id[6] = ++num = 3;

至此，强联通分量全部找出;

以上；