Codeforces Round #613 (Div. 2) A-E简要题解

contest链接：https://codeforces.com/contest/1285

A. Mezo Playing Zoma

签到

 #include<iostream>
 #include<vector>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<queue>
 #include<map>
 using namespace std;
 const int maxn = ;
 typedef long long ll;
 queue<pair<int,int> > q;
 map<int,bool> vis;
 vector<int> v;
 /*
 1111111111111111111111111111111111111
 */
 int a[maxn];
 int main()
 {
    int n;
    cin>>n;
    string s;
    cin>>s;
    int n1=,n2=;
    for(int i=;i<s.size();i++)
    {
        if(s[i]=='L')
         n1++;
        if(s[i]=='R')
         n2++;
    }
     cout<<n2+n1+;
     return ;
 }

B. Just Eat It!

 #include <bits/stdc++.h>
 using namespace std;
 #define finish(x) return cout << x << endl, 0
 #define ll long long

 int n;
 vector <int> a;

 bool solve(){
     cin >> n;
     a.resize(n);
     for(auto &i : a) cin >> i;
     ll sum = ;
     for(int i =  ; i < n ; i++){
         sum += a[i];
         if(sum <= ) return ;
     }
     sum = ;
     for(int i = n -  ; i >=  ; i--){
         sum += a[i];
         if(sum <= ) return ;
     }
     return ;
 }
 int main(){
     ios_base::sync_with_stdio();
     cin.tie();
     int T;
     cin >> T;
     while(T--){
         if(solve()) cout << "YES\n";
         else cout << "NO\n";
     }
 }

C. Fadi and LCM

题意：给一个整数X（1~10^12），找到两个数a,b，使得LCM（a,b） = X，且max（a,b）尽可能地小。

思路：LCM(a,b) = X，则a，b必是X的因子，那么对于X，除去他自己本身，最大的因子不会超过√x，且对于X始终会存在一对a,b互素，LCM（a,b） = X。所以枚举a从√x开始，如果再计算n/a = b，若gcd（a,b） = 1，则就是使得max（a,b）尽可能小的答案了。

AC：

 #include<iostream>
 #include<vector>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<queue>
 #include<map>
 using namespace std;
 const int maxn = ;
 typedef long long ll;
 ll gcd(ll a, ll b){ return b?gcd(b,a%b):a; }
 ll lcm(ll a, ll b){ return a/gcd(a,b)*b; }
 vector<ll> v1;
 int main()
 {
     ll a,b;
     ll n;
     cin>>n;
     for(int i = sqrt(n);i>=;i--){
         if(n%i == ){
             if(gcd(i,n/i) == ){
                 cout<<i<<" "<<n/i;
                 return ;
             }
         }
     }
     cout<<<<" "<<n;
     return ;
 }

D. Dr. Evil Underscores

题意：给n个数a₁，a₂，a₃.....a_n，找到一个数X，使得X 异或所有的a_i ，得到的max（X xor a_i）最小，输出这个值。

思路：a的范围是0~2³⁰，我们可以以01二进制的形式建一棵深度为30的字典树，每个数a_i 的二进制序列插入到字典树中去，例如5 = 101，那么101按位插入到字典树中去。然后从根开始遍历，在字典树上dp，因为该字典树建完后是一棵二叉树，所以分支情况就两种，下一位是0或1，那么如果只遇到1就往1这个分支走，这一位便没有贡献，如果只遇到0就往0这个分支走，这一位也没有贡献，如果遇到的是0和1两个分支，那么必定要加上这一位的贡献，然后递归01两个分支，两者再去min，一直递归到最后一位。

AC代码：

 #include<iostream>
 #include<vector>
 #include<cstdlib>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<queue>
 #include<map>
 using namespace std;
 typedef long long ll;
 int trie[][],cnt ;
 //bool exist[31*31];// 该结点结尾的字符串是否存在
 void insert(int a){//建trie树
     int p = ;
     for(int i = ;i>=;i--){
         int c = (a>>i)&;
         if(!trie[p][c]) trie[p][c] = ++cnt; // 如果没有，就添加结点
         p = trie[p][c];
     }
 //    exist[p] = 1;
 }
 ll solve(ll cur,int k){
     if(k == -) return ;
     if(trie[cur][] == ){
         return solve(trie[cur][],k-);//如果只有1分支
     }
     else if(trie[cur][] == ){//如果只有0分支
         return solve(trie[cur][],k-);
     }
     else{
         return (<<k)+min(solve(trie[cur][],k-),solve(trie[cur][],k-));//0 1分支都有的情况
     }
 }
 int main()
 {
     int n;
     cin>>n;
     for(int i = ;i<n;i++){
         ll a;cin>>a;
         insert(a);
     }
     ll ans = solve(,);
     cout<<ans;
     return ;
 }

E. Delete a Segment

题意：给一个数轴上有n个线段集，线段集若有相交，则合并为一个新的合并线段集，比如[1,6]和[2,9]，因为两个线段有相交，所以要合并为[1,9]，先问删掉给定的n个线段集中的任意一个，剩下的n-1个线段组成的新的合并线段集数量最大是多少？

思路：

这道题首先想到的是并查集做法，枚举删除任意一条线段后，剩下的线段组成的集合是多少，取max，这个复杂度有n² × 并查集复杂度，显然是不行的。那么考虑离散化处理线段左右端点，然后去扫描。

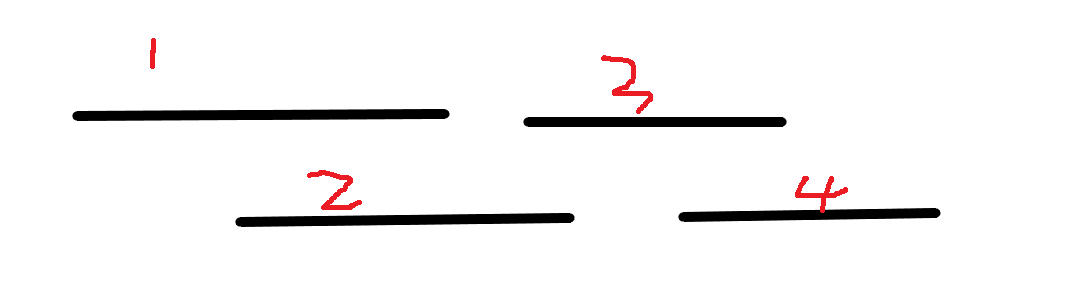
如图所示，线段1，2，3，4离散化处理左右端点，然后排个序并标记一下线段号，开始扫描，扫描到的端点先放入multiset集合中去，最初扫描到线段1的左端点L₁，然后是L₂，再然后是R₁，此时我们发现，线段1已经扫描完比，那么删除这条线段1的左右端点，发现集合中只剩下了L₂，且下一个要扫描到的端点是L₃，此时就意味着删除点线段2后，线段1和线段3是不相交的，那么删除线段2后，新线段合并集合数量就会+1。同理当扫描到R₂时，整个线段2已经扫描完毕，删除集合中线段2左右端点，集合只剩下线段3的左端点，且下一个元素是线段4的左端点，说明线段2和线段4不相交，那么此时删除线段3，就意味着线段2和线段4不相连，新线段合并集合数量就+1，根据以上这个性质，扫描的时候枚举下个元素是左端点还是右端点，记录删除每个线段删除后，合并集合会增加多少，最终拿最初不删除任何线段得到的合并线段集数量+max（删除某一线段增加的数量）就是答案

当然要特判一种情况：

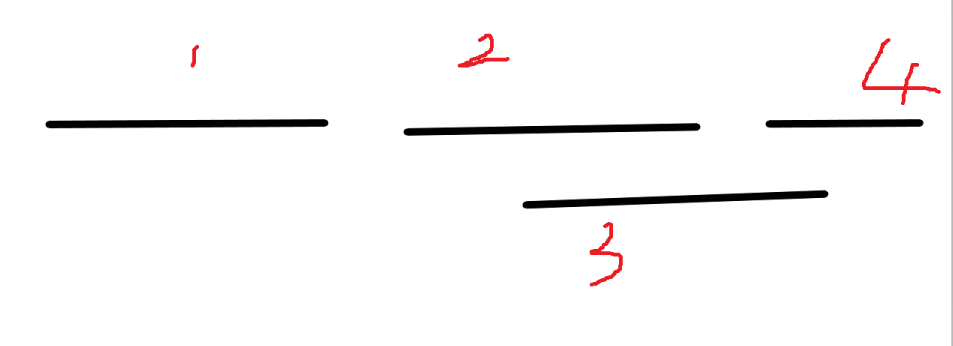
如图所示线段1这种情况，删除这条线段，则新合并集是-1，因为它没有和任何线段有相交，本身就构成一个独立的合并线段集，删除就减少1个合并线段集，特判这种情况即可。

AC代码：

 #include<iostream>
 #include<vector>
 #include<cstdlib>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<set>
 #include<cstring>
 #include<queue>
 #include<map>
 using namespace std;
 typedef long long ll;
 const int maxn = 4e5+;
 pair<ll,ll> p[maxn];
 int cnt[maxn];
 int main()
 {
     int t;
     cin>>t;
     while(t--){
         int n;
         cin>>n;
         for(int i = ;i<=n;i++){
             ll l,r;
             cin>>l>>r;
             p[*i-] = make_pair(l,-i);//离散化记录区间左右端点的位置和区间标号i
             p[*i] = make_pair(r,i);
             cnt[i] = ;
         }
         sort(p+,p+*n+);
         int ans = ;
         multiset<int> s;
         for(int i = ;i<=*n;i++){
             if(p[i].second < ){//如果是左端点，就插入set
                 s.insert(-p[i].second );
             }
             else{
                 s.erase(s.find(p[i].second));//如果是右端点，就把这个区间删除
             }
             if(s.size() == ) ans++;//如果集合是空，记录一个合并的区间
             if(s.size() ==  && p[i].second >  && p[i+].second <  && p[i+].first > p[i].first ){
                 cnt[*s.begin()]++;//当前是左端点，但是下个是右端点，cnt++
             }
             if(s.size() ==  && p[i].second <  && p[i+].second >){
                 cnt[*s.begin()]--;//特判，如果首先插入地是一段单独区间（l r），去掉这个区间则区间数量-1
             }
         }
         int t = -;
         for(int i = ;i<=n;i++){
             t = max(t,cnt[i]);
         }
         cout<<ans+t<<endl;
     }
     return ;
 }