判断强联通图中每条边是否只在一个环上（hdu3594）

hdu3594

Cactus

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 1131    Accepted Submission(s): 542

Problem Description

1. It is a Strongly Connected graph.

2. Each edge of the graph belongs to a circle and only belongs to one circle.

We call this graph as CACTUS.








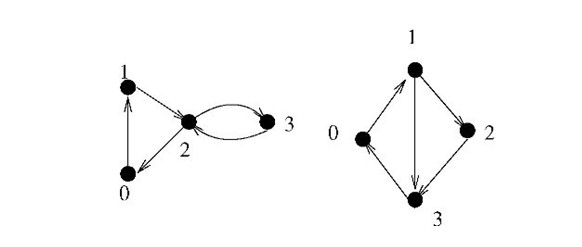
There is an example as the figure above. The left one is a cactus, but the right one isn’t. Because the edge (0, 1) in the right graph belongs to two circles as (0, 1, 3) and (0, 1, 2, 3).

 

Input

The input consists of several test cases. The first line contains an integer T (1<=T<=10), representing the number of test cases.

For each case, the first line contains a integer n (1<=n<=20000), representing the number of points.

The following lines, each line has two numbers a and b, representing a single-way edge (a->b). Each case ends with (0 0).

Notice: The total number of edges does not exceed 50000.

 

Output

For each case, output a line contains “YES” or “NO”, representing whether this graph is a cactus or not.

 

Sample Input

2
4
0 1
1 2
2 0
2 3
3 2
0 0
4
0 1
1 2
2 3
3 0
1 3
0 0
题意：


1：强连通图

2：图中每条边只处于一个环内

怎么样判断一个边只在一个环内呢？其实在没有找到一个环之前的时候，有一个DFS的过程，在这个过程中每走到一个点，我们就记录一下它是有哪一个点走下来的 也就是这个点的上一层的点，等到我们找到环的时候，我们马上返回去查找，查找那个点是 out了两次以上，那么肯定有边处于两个或者两个以上环内，就不符合了
#include"stdio.h"
#include"string.h"
#include"queue"
#include"stack"
#include"iostream"
#include"stdlib.h"
#define M 20005
#define inf 999999999
using namespace std;
stack<int>q;
int head[M],dfn[M],low[M],use[M],belong[M],pre[M],sum[M],flag1;
int num,index,t,n;
struct st
{
    int u,v,next;
}edge[M*3];
void init()
{
    t=0;
    memset(head,-1,sizeof(head));
}
void add(int u,int v)
{
    edge[t].u=u;
    edge[t].v=v;
    edge[t].next=head[u];
    head[u]=t++;
}
void tarjan(int u)
{
    int i;
    dfn[u]=low[u]=++index;
    q.push(u);
    use[u]=1;
    for(i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].v;
        if(!dfn[v])
        {
            pre[v]=u;
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(use[v])
        {
            low[u]=min(low[u],dfn[v]);
            for(int j=u;j!=v;j=pre[j])//当发现后向边指向祖先点的时候，
            //就顺着环向上查找，把点记录在sum++中，若有点被记录了两次
            //或两次以上，则返回，肯定有边至少在两个环内；
            {
                sum[j]++;
                if(sum[j]>1)
                {
                    flag1++;
                    break;
                }
            }
        }

    }
    if(dfn[u]==low[u])
    {
        num++;
        int vv;
        do
        {
            vv=q.top();
            q.pop();
            use[vv]=0;
            belong[vv]=num;
        }while(vv!=u);
    }
}
void solve()
{
    num=index=0;
    int i;
    memset(belong,-1,sizeof(belong));
    memset(dfn,0,sizeof(dfn));
    memset(use,0,sizeof(use));
    memset(pre,0,sizeof(pre));
    memset(sum,0,sizeof(sum));
    for(i=1;i<=n;i++)
    {
        if(!dfn[i])
        {
            tarjan(i);
        }
    }
}
int main()
{
    int T,i;
    scanf("%d",&T);
    while(T--)
    {
        init();
        scanf("%d",&n);
        int x,y;
        while(scanf("%d%d",&x,&y),x||y)
        {
            x++;
            y++;
            add(x,y);
        }
        flag1=0;
        solve();
        int flag=0;
        for(i=1;i<=n;i++)
        {
            if(belong[i]!=belong[1])
            {
                flag++;
                break;
            }
        }
        if(flag)
            printf("NO\n");
        else
        {
            if(flag1)
                printf("NO\n");
            else
                printf("YES\n");
        }

    }
}