Codeforces 834D - The Bakery（dp+线段树）

834D - The Bakery

思路：dp[i][j]表示到第j个数为止分成i段的最大总和值。

dp[i][j]=max{dp[i-1][x]+c(x+1,j)(i-1≤x≤j-1)}，c(x+1,j)表示x+1到j的不同的值。

用线段树维护一下最大值。

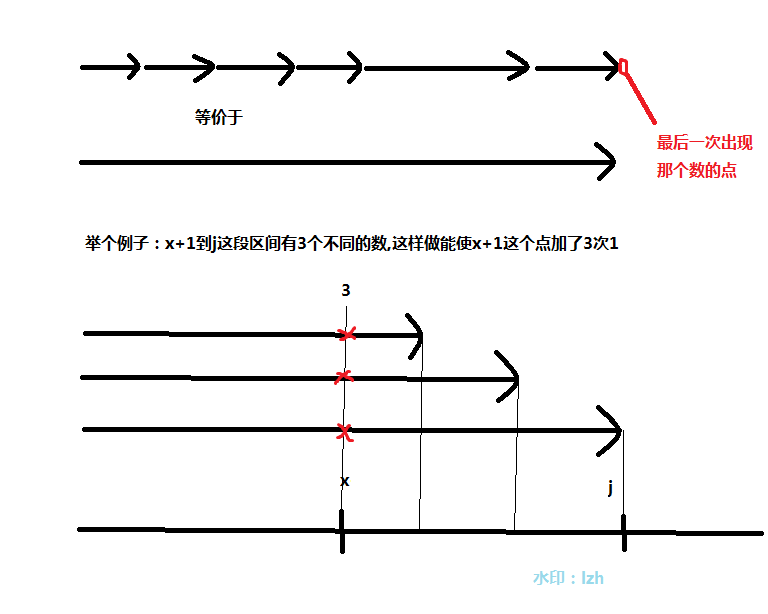
上图最后一个点取不到，不解释，不明白请评论。

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ls rt<<1,l,m
#define rs rt<<1|1,m+1,r
#define pb push_back
const int INF=0x3f3f3f3f;
const int N=;
int tree[*N],lazy[*N];
int dp[][N];
int now[N],pre[N],a[N];
int i;

void push_up(int rt)
{
    tree[rt]=max(tree[rt<<],tree[rt<<|]);
}

void push_down(int rt)
{
    tree[rt<<]+=lazy[rt];
    lazy[rt<<]+=lazy[rt];
    tree[rt<<|]+=lazy[rt];
    lazy[rt<<|]+=lazy[rt];
    lazy[rt]=;
}

void build(int rt,int l,int r)
{
    if(l==r)
    {
        tree[rt]=dp[i-][l];
        return ;
    }
    int m=(l+r)>>;
    build(ls);
    build(rs);
    push_up(rt);
}

void update(int p,int delta,int rt,int l,int r)
{
    if(l==r)
    {
        tree[rt]+=delta;
        return ;
    }
    int m=(l+r)>>;
    if(p<=m)update(p,delta,ls);
    else update(p,delta,rs);
    push_up(rt);
}

void Update(int L,int R,int delta,int rt,int l,int r)
{
    if(L<=l&&r<=R)
    {
        tree[rt]+=delta;
        lazy[rt]+=delta;
        return ;
    }
    if(lazy[rt])push_down(rt);
    int m=(l+r)>>;
    if(L<=m)Update(L,R,delta,ls);
    if(R>m)Update(L,R,delta,rs);
    push_up(rt);
}

int query(int L,int R,int rt,int l,int r)
{
    if(L<=l&&r<=R)return tree[rt];
    if(lazy[rt])push_down(rt);
    int m=(l+r)>>,ans=;
    if(L<=m)ans=max(ans,query(L,R,ls));
    if(R>m)ans=max(ans,query(L,R,rs));
    return ans;
}

int main()
{
    int n,k;
    while(~scanf("%d%d",&n,&k))
    {
        memset(now,,sizeof(now));
        for(int i=;i<=n;i++)
        {
            cin>>a[i];
            pre[i]=now[a[i]];
            now[a[i]]=i;
        }
        dp[][]=;
        for(i=;i<=k;i++)
        {
            memset(tree,,sizeof(tree));
            memset(lazy,,sizeof(lazy));
            build(,,n);
            for(int j=i;j<=n;j++)
            {
                Update(pre[j],j-,,,,n);
                dp[i][j]=query(i-,j-,,,n);
            }
        }
        cout<<dp[k][n]<<endl;
    }
    return ;
}