关于FFT分析音频的学习

本文部分知识从以下文章学习：

https://zhuanlan.zhihu.com/p/19763358 傅里叶变换的知识

https://www.cnblogs.com/RabbitHu/p/FFT.html FFT的知识

最近工作上在做关于音乐游戏的内容，其中需要分析音频找节奏点（或者说是重音点）。

学习了一系列相关知识后，了解到一段音乐的波形图可以分解成不同频率的波形图，也就是由时域到频域的转换。

借用其他博主的图就比较容易理解了，如下所示。

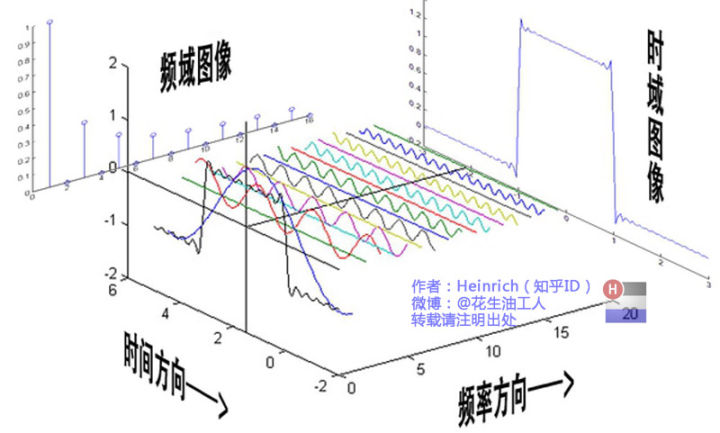
波从时域到频域的转换可以通过傅里叶变换实现，关于傅里叶变换的知识可以从最上面的链接学习或者自行查找（傅里叶真厉害！！！）。

计算机处理的音频在时域上是离散的数据，我们可以使用离散傅里叶变换DFT（傅里叶变换在时域和频域上都呈离散的形式）获得频域上的离散数据。

快速傅立叶变换FFT是DFT的快速算法，其核心思路就是分治法的DFT，具体推导可以查看上面的第二个链接。

FFT 代码如下：

　　　　 static void BitReverse(Complex[] cpData, int n)
        {
            Complex temp;
            int lim = ;
            while (( << lim) < n) lim++;
            for (int i = ; i < n; i++)
            {
                int t = ;
                for (int j = ; j < lim; j++)
                {

                    if (((i >> j) & ) != )
                        t |= ( << (lim - j - ));
                }
                if (i < t)
                {
                    temp = cpData[i];
                    cpData[i] = cpData[t];
                    cpData[t] = temp;
                } // i < t 防止交换两次
            }
        }

        static void FFT1(Complex[] cpData, bool forward)
        {
            var n = cpData.Length;

            BitReverse(cpData, n);//位反转

            Complex[] omg = new Complex[n];
            for (int i = ; i < n; i++)
            {
                omg[i] = new Complex((float)Math.Cos( * Math.PI * i / n), (float)Math.Sin( * Math.PI * i / n));
            }
             Complex temp ;
            for (int step = ; step <= n; step *= )
            {
                int m = step / ;
                for (int j = ; j < n; j += step)
                    for (int i = ; i < m; i++)
                    {//蝶形运算
                        if(forward)
                            temp = omg[n / step * i] * cpData[j + i + m];
                        else
                            temp = omg[n / step * i].Conjugate() * cpData[j + i + m];
                        cpData[j + i + m] = cpData[j + i] - temp;
                        cpData[j + i] = cpData[j + i] + temp;
                    }
            }
        }

Complex是封装的复数类，偷懒不是自己写的，来自这位老哥https://blog.csdn.net/u011583927/article/details/46974341

这个FFT，new了好多对象，效率不是很高。。。

再贴一个直接把复数的实部虚部轮流放在一个数组里直接算的，能快一些。

　　　　 static void Reverse(float[] data, int n)
        {

            int j = , k = ;
            var top = n / ;
            while (true)
            {

                var t = data[j + ];
                data[j + ] = data[k + n];
                data[k + n] = t;
                t = data[j + ];
                data[j + ] = data[k + n + ];
                data[k + n + ] = t;
                if (j > k)
                {
                    t = data[j];
                    data[j] = data[k];
                    data[k] = t;
                    t = data[j + ];
                    data[j + ] = data[k + ];
                    data[k + ] = t;

                    t = data[j + n + ];
                    data[j + n + ] = data[k + n + ];
                    data[k + n + ] = t;
                    t = data[j + n + ];
                    data[j + n + ] = data[k + n + ];
                    data[k + n + ] = t;
                }

                k += ;
                if (k >= n)
                    break;

                var h = top;
                while (j >= h)
                {
                    j -= h;
                    h /= ;
                }
                j += h;
            }
        }
        static void FFT2(float[] data, bool forward)
        {
            var n = data.Length;
            n /= ;

            Reverse(data, n);

            float sign = forward ?  : -;
            var mmax = ;
            while (n > mmax)
            {
                var istep =  * mmax;
                var theta = sign * (float)Math.PI / mmax;
                float wr = , wi = ;
                var wpr = (float)Math.Cos(theta);
                var wpi = (float)Math.Sin(theta);
                for (var m = ; m < istep; m += )
                {
                    for (var k = m; k <  * n; k +=  * istep)
                    {
                        var j = k + istep;
                        var tempr = wr * data[j] - wi * data[j + ];
                        var tempi = wi * data[j] + wr * data[j + ];
                        data[j] = data[k] - tempr;
                        data[j + ] = data[k + ] - tempi;
                        data[k] = data[k] + tempr;
                        data[k + ] = data[k + ] + tempi;
                    }
                    var t = wr;
                    wr = wr * wpr - wi * wpi;
                    wi = wi * wpr + t * wpi;
                }
                mmax = istep;
            }

        }

　　　　 static void Main(string[] args)
        {

            int n =*;
            float[] data = new float[ * n];
            for (int i = ; i < n; i++)
            {
                data[ * i] = i;
                data[ * i + ] = ;
            }

            Complex[] cpData = new Complex[n];
            for (int i = ; i < n; i++)
            {
                cpData[i] = new Complex(data[ * i], data[ * i + ]);
            }

            long s = DateTime.Now.Ticks;
            FFT1(cpData, true);
            Console.WriteLine("time:" + (DateTime.Now.Ticks - s) / );

            s = DateTime.Now.Ticks;
            FFT2(data, true);
            Console.WriteLine("time:" + (DateTime.Now.Ticks - s) / );

            Console.Read();
        }

速度上还是差挺多的。。。

好了获得频率数据之后的流程就不再那么烧脑了（都怪自己早早把傅里叶变换还给课本了）。。。

找节奏点的逻辑大概如下（代码有点多就不贴了）：

1.根据采样率依次获取数据，每次通过FFT得到一组复数数组。

2.计算出复数的模长，可以表示此频率下的声音大小，可以把一定范围的声音累加起来，可以用来表示低音、中音、高音。

3.对比每一帧的数据变化就可以判断出节奏点（声音变化大，可以表示是一个节奏点）。

其实能得到频域的值，针对不同的功能，大家后面就可以自由发挥了。